快读没打符号,100->35(竟然还得了35)
在直角坐标系上,有N个边平行于坐标轴的矩形。你的任务是把其中的K个矩形染色,使按次序放下后,可以看见的有色面积最大。可看见的意思就是这一部分没有被后面的矩形覆盖。
你的答案是返回K个整数,表示你染色的是哪K个矩形。如果有多种答案,输出字典序最小的。
1<=N<=50; 1<=K<=N。
每个坐标值为[-10000,10000]之间的整数。
第一行两个整数:N K
后面有N行,每行4个整数: x1 y1 x2 y2, 分别表示先后各个矩形的左下角坐标和右上角坐标。
一行,K个整数:你的方案。
|
输入 |
3 2 1 1 5 3 3 2 7 4 2 5 9 7 |
7 4 1 1 5 4 2 2 4 3 4 0 6 2 7 1 9 4 1 5 4 7 6 5 9 7 2 5 8 6 |
|
输出 |
1 2 |
0 2 3 6 |
样例解释:
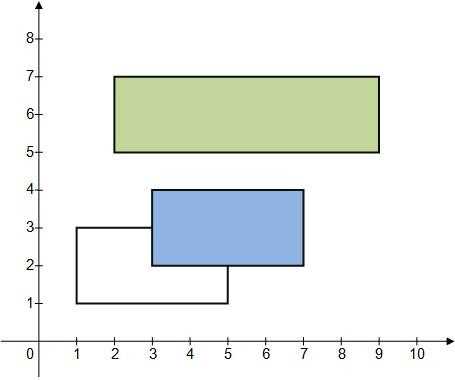
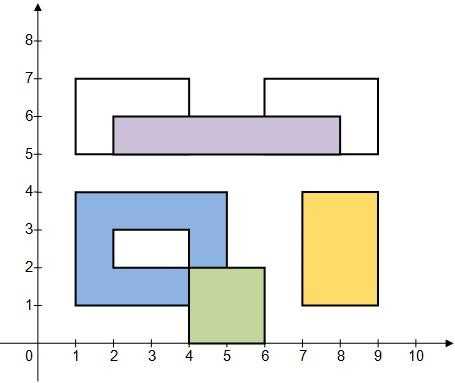
我们可以用类似扫描线的思路:(有些暴力)
先将横坐标离散化,然后依次对离散化的每个区间:枚举每个包含这个区间的矩形,从上往下覆盖,记录已经被覆盖的纵坐标,那么就不能将这些已经被覆盖的点计算到下面的矩形的面积里。(线段树维护也是资瓷的)
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #define R register int using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix;; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } struct node{int x1,x2,y1,y2;}a[55]; struct Node{int s,rk; bool operator <(const Node& y)const{return s==y.s?rk<y.rk:s>y.s;} }ans[55]; int n,k,cnt,tot; int xx[110],rw[110],anss[55]; bool vis[20010],*v=vis+10001; signed main() { freopen("color.in","r",stdin); freopen("color.out","w",stdout); n=g(),k=g(); for(R i=1;i<=n;++i) a[i].x1=g(),a[i].y1=g(),a[i].x2=g(),a[i].y2=g(),ans[i].rk=i-1; for(R i=1;i<=n;++i) xx[++cnt]=a[i].x1,xx[++cnt]=a[i].x2; sort(xx+1,xx+cnt+1); tot=unique(xx+1,xx+cnt+1)-xx-1; //cout<<"!!!cnt: "<<cnt<<" !!!tot:"<<tot<<endl; for(R i=1;i<=tot;++i) rw[i]=xx[i];//,cout<<xx[i]<<" "; cout<<endl; for(R i=1;i<tot;++i) { memset(vis,0,sizeof(vis)); //for(R j=1,len=0;j<=n;++j,len=0) {if(a[j].x1<=rw[i]&&a[j].x2>=rw[i+1]) for(R j=n,len=0;j>=1;--j,len=0) {if(a[j].x1<=rw[i]&&a[j].x2>=rw[i+1]) for(R k=a[j].y1+1;k<=a[j].y2;++k) if(!v[k]) ++len,v[k]=true;//cout<<"fasdjfasdff"<<k<<endl; ans[j].s+=len*(rw[i+1]-rw[i]); } } //for(R i=1;i<=n;++i) cout<<ans[i].s<<" "<<ans[i].rk<<endl; sort(ans+1,ans+n+1); for(R i=1;i<=k;++i) anss[i]=ans[i].rk; sort(anss+1,anss+k+1); for(R i=1;i<=k;++i) printf("%d ",anss[i]); //while(1); }
2019.05.08 记住这回的耻辱
原文:https://www.cnblogs.com/Jackpei/p/10835911.html