最近在重拾物理,今日在和同事吃饭时,与其聊到了如何测量地球距离某个观测到的外太空星球的距离的问题,谈到了三角测量法
三角测量法:
用地球关于太阳公转的二点A, B与太阳在同一直线L上,测量在A、B两点与测距星球的角度,进而使用余弦定理(弦竟然是念xian,念了十多年的xun,果然汉语是数学老师教的)即可得到
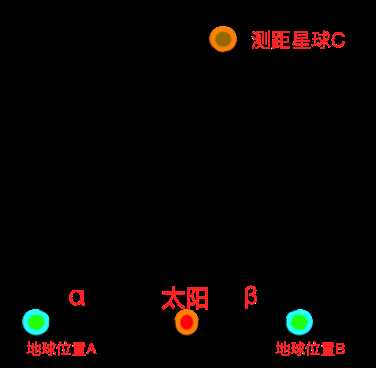
如上图,如果A、B、C三点在同一平面上,则符合欧氏空间(可将A、B、C选取为球体质心),便可采用余弦定理,这里已知的量有
二个夹角α, β,所夹的边AB,由相似三角形可知,这可唯一确定一个三角形,需要求出另外两边AC, AB
由余弦定理有
BC2 = AB2 + AC2 - 2AB*ACcosα
AC2 = AB2 + BC2 - 2AB*BCcosβ
其中只有AC、BC未知,故此为二次二元方程组,有解,可计算出BC, AC的值,如果星球距离远大于AB,那么BC, AC应该相差不多 ,则可以当作等腰三角形进行估算
曲面上的三角测量并不符合欧氏空间,犹如地球表面是曲面,并不是平面,也就可以推测地球是曲的不是平的
同事便问道,又如何测量AB的距离,也就是地球与太阳的距离,当时有些懵懂,吃完饭后,静下来思索起来
隐约想起来以前上学测试山峰的海拔,具体的测量方法却是想不起来了,便就自己琢磨起来
如果拉线直接测,不是想要的,而我又知道什么呢?只有太阳光,还有数学,于是想到了如下的图案

先说明测量的可行性,杆子可以这样摆放,因为垂直线在AB上从0增大到BC,也已知杆子的长度远小于山峰的高度, 即DB << BC,同样对于FH有同样的结论,因此测量是可行的
采用相似三角形建立方程
AD/AB = AD/(AD+DB) = DG/BC
EF/EB = EF/(DB - DE) = FH/BC = DG/BC
解得
DB = (DE+EF)AD/(AD-EF)
BC = (DE+EF)DG/(AD-EF)
这里AD ≠ EF, 因为如果AD=EF,有DG= FH,则三角形ADG全等于三角形EFH,角GAD = 角HEF= 角GAD + 角ACE,因此A、E重合,故方程组必有解
回归正题,于是乎想想能不能通过太阳光粗略估算地球与太阳的距离,毕竟三角测量法也是根据光进行测量的,故脑海里有了如下图案

先说明可测性,可以想象太阳如地球公转的圆心,通过再架AE、BD两根杆子可测得夹角α和β
易看出这个正好符号三角测量法,即角α和β和其夹边AB
以上皆是估算,注重数学方法的运用,因为个人懒惰成性,手不想解出关于余弦定理的方程组的解。
原文:https://www.cnblogs.com/sangdesu/p/10839834.html