如题,给出两个字符串s1和s2,其中s2为s1的子串,求出s2在s1中所有出现的位置。
为了减少骗分的情况,接下来还要输出子串的前缀数组next。
(如果你不知道这是什么意思也不要问,去百度搜[kmp算法]学习一下就知道了。)
输入格式:
第一行为一个字符串,即为s1
第二行为一个字符串,即为s2
输出格式:
若干行,每行包含一个整数,表示s2在s1中出现的位置
接下来1行,包括length(s2)个整数,表示前缀数组next[i]的值。
说明
时空限制:1000ms,128M
设s1长度为N,s2长度为M
对于30%的数据:N<=15,M<=5
对于70%的数据:N<=10000,M<=100
对于100%的数据:N<=1000000,M<=1000000
样例说明:
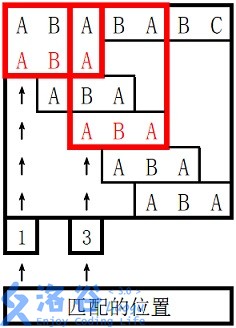
所以两个匹配位置为1和3,输出1、3
本来还想用暴力算法去做这道题,结果看到这个玄学的防骗分方式后,果断选择花两个小时学习KMP,顺便orz%%%了SRY大佬~~~
KMP基本思想:
比如,在简单的一次匹配失败后,我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的:在已经匹配的模式串子串中,找出最长的相同的前缀和后缀,然后移动使它们重叠。(摘自百度百科)
之后我们就可以开心的开始敲代码辣~~~首先我们要考虑的是如何找到最长的相同前缀后缀,最朴素的算法是O(n2)(n为模式串长度(等待匹配的串A为文本串,进行匹配的串B为模式串))
我们来想一想如何优化:首先,在算P[i]之前(p[i]代表模式串前i位字符最长相同前缀后缀),我们已知的是p[0...i-1];我们可以用递推的方法去求解。
和一般的递推方法不同的是,这个递推并没有固定的递推式,网上有许多人说是“自己匹配自己”,而我并不这么认为。。。蒟蒻和大佬的思维果然不一样,再次orz%%%
举一个简单的栗子~:abaa,p[1]=0,p[2]=0,p[3]=1,下面我们重点看一下如何算p[4];由于前边第一个a和第三个a已经匹配成功,如果2个字符和当前字符可以匹配的话,那么直接加上1就好了;
重点在于不能匹配的情况,这也是本蒟蒻学习KMP最大的障碍。匹配失败,证明当前的前缀后缀位数太多了,匹配不上,所以我们要减小前缀的数目,所以我们要在这个前缀里再找前后缀,看到p[1]=0,所以我们直接看第1个和当前字符能不能匹配即可。发现匹配成功,于是乎p[4]=1;推广到一般情况:设正在计算第i号字符对应的p[i]值,先去找前i-1个字符的最长相同前后缀(p[i-1]),设p[i-1]=j,然后如果b[j+1]==b[i],则p[i]=j+1;否则顺着失配边走,走到可以匹配或者确定无法匹配位置,对应着下面这段代码:
for(int i=2;i<=m;i++)
{
while(j>0&&b[i]!=b[j+1])j=p[j];//好好体会这个while循环,失配的精髓。
if(b[i]==b[j+1])j++;
p[i]=j;
}
预处理完p数组后,我们就可以开始正式匹配了,结合百度百科的基本思想可以体会到,KMP之所以会省时间,是因为它实际上是一个动态选取最优值的过程,它很好地利用了前缀的性质,没有无用功。
当不可以匹配的时候,朴素算法是右移一位,而KMP能移多少移多少,也就是所谓的自我匹配。
#include<iostream>
#include<cstring>
using namespace std;
char a[1000010],b[1000010];
int n,m,p[1000010],j;
int main()
{
cin>>a+1;
cin>>b+1;
n=strlen(a+1);
m=strlen(b+1);
for(int i=2;i<=m;i++)
{
while(j>0&&b[i]!=b[j+1])j=p[j];
if(b[i]==b[j+1])j++;
p[i]=j;
}
j=0;
for(int i=1;i<=n;i++)
{
while(j>0&&a[i]!=b[j+1])j=p[j];//失配
if(a[i]==b[j+1])j++;
if(j==m)
{
cout<<i-m+1<<endl;
j=p[j];//继续匹配
}
}
for(int i=1;i<=m;i++)
{
cout<<p[i]<<" ";
}
return 0;
}
原文:https://www.cnblogs.com/szmssf/p/10840741.html