问题

在一个圆环上随机取3点，求这3个点组成一个锐角三角形的概率

题解

如下图所示：

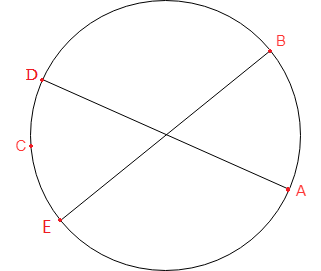
取单位圆上任意两点点A和B，A、B两点确定以后，点A、B、C三点要够成锐角三角形，点C必须在DE之间，否在将构成直角三角形（点C与点D或点E重合）或钝角三角形。设AB弧所对应的圆心角为\(\theta\),则当且仅当\(\theta \in (0, \pi)\) 时有可能构成锐角三角形。\(\theta\) 的概率密度是 \(\frac{1}{\pi}\)，此时组成锐角三角形需要C点在AB对应的DE段间的概率是 \(\frac{\theta}{2\pi}\)。故在一个圆环上随机添加3点，三个点组成一个锐角三角形的概率为
\[\int_0^\pi \frac{1}{\pi}\cdot\frac{\theta}{2\pi}\mathrm{d}\theta = \frac{\theta ^ 2}{4\pi ^ 2}\bigg|_0^\pi = \frac{1}{4}\]

Python 代码模拟

#! /usr/bin/env python3
# -*- coding: utf-8 -*-

# @Author: wzdnzd

import numpy as np


def simulate(n):
    # 圆心角θ所对应的弦长 l = 2 * R * sin(θ/2), R为圆的半径
    def compute(theta):
        if theta > np.pi:
            theta = 2 * np.pi - theta

        return 2 * np.sin(theta / 2)

    # 根据三角形三条边的平方关系判断是否是锐角、直角或钝角三角形
    def judge(array):
        if len(array) != 3:
            raise ValueError('len(array) must be 3.')

        if array[0] ** 2 + array[1] ** 2 > array[2] ** 2:
            return -1
        elif array[0] ** 2 + array[1] ** 2 == array[2] ** 2:
            return 0
        else:
            return 1

    acute, right, obtuse = 0, 0, 0
    for _ in range(n):
        angles = sorted(np.random.rand(3) * 2 * np.pi)
        chords = sorted([compute(angles[1] - angles[0]),
                         compute(angles[2] - angles[1]), 
                         compute(2 * np.pi + angles[0] - angles[2])])

        flag = judge(chords)
        if flag == -1:
            acute += 1
        elif flag == 0:
            right += 1
        else:
            obtuse += 1

    return [x / n for x in [acute, right, obtuse]]


if __name__ == "__main__":
    probabilities = simulate(100000)
    print('acute: {}\tright: {}\tobtuse: {}'.format(
        probabilities[0], probabilities[1], probabilities[2]))

运行结果如下：

acute: 0.25009  right: 0.0      obtuse: 0.74991

数理统计 - 圆环上随机取3个点组成一个锐角三角形的概率

原文：https://www.cnblogs.com/betabear/p/10807597.html