hdu3338 / 方格横纵和问题终极版，最大流斩

此题被誉为神奇最大流，诱惑我去做了下，感觉也是通常的思路。

题意：1.用1-9去填，满足所给的行/列和要求（和那个什么游戏差不多。。。）

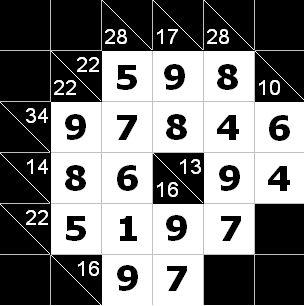
一看，直接就建图了，每个点在白色的点中间，由横和=纵和，管理横和的在左边，纵和的点在右边。S->横和点，纵和点到t，建图即可。

有一点注意，由于只能用1-9去填，是有上下界的网络流问题，所以这里有点比较巧妙，所有白色的点都减去1，和也对应减去几。用0做1,1做2...8做9.一一对应，实现转移为一般最大流问题。最后再加一即可。

#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxv=20100,maxe=1000101;
int nume=0;int head[maxv];int e[maxe][3];
void inline adde(int i,int j,int c)
{
    e[nume][0]=j;e[nume][1]=head[i];head[i]=nume;
    e[nume++][2]=c;
    e[nume][0]=i;e[nume][1]=head[j];head[j]=nume;
    e[nume++][2]=0;
}
int ss,tt,n,m;
int vis[maxv];int lev[maxv];
bool bfs()
{
    for(int i=0;i<maxv;i++)
      vis[i]=lev[i]=0;
    queue<int>q;
    q.push(ss);
    vis[ss]=1;
    while(!q.empty())
    {
        int cur=q.front();
        q.pop();
        for(int i=head[cur];i!=-1;i=e[i][1])
        {
            int v=e[i][0];
            if(!vis[v]&&e[i][2]>0)
            {
                lev[v]=lev[cur]+1;
                vis[v]=1;
                q.push(v);
            }
        }
    }
    return vis[tt];
}
int dfs(int u,int minf)
{
    if(u==tt||minf==0)return minf;
    int sumf=0,f;
    for(int i=head[u];i!=-1&&minf;i=e[i][1])
    {
        int v=e[i][0];
        if(lev[v]==lev[u]+1&&e[i][2]>0)
        {
            f=dfs(v,minf<e[i][2]?minf:e[i][2]);
            e[i][2]-=f;e[i^1][2]+=f;
            sumf+=f;minf-=f;
        }
    }
    if(!sumf) lev[u]=-1;
    return sumf;
}
int dinic()
{
    int sum=0;
    while(bfs())sum+=dfs(ss,inf);
    return sum;
}
struct cell         //方块
{
     int clour;
     int x,y;
};
cell ces[102][102];
void read_build()
{
    string ts;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            cin>>ts;
            if(ts=="XXXXXXX")      //黑色
              {
                  ces[i][j].clour=0;
                  ces[i][j].x=ces[i][j].y=-1;
              }
            else if(ts==".......")   //白色
            {
                 ces[i][j].clour=5;
                 ces[i][j].x=ces[i][j].y=0;
            }
            else if(ts[0]=='X'&&ts[4]!='X')    //横向要填
            {
                 ces[i][j].clour=2;
                 ces[i][j].x=((ts[4]-'0')*10+(ts[5]-'0'))*10+(ts[6]-'0');
                 ces[i][j].y=-1;
            }
             else if(ts[0]!='X'&&ts[4]=='X')   //纵向要填
            {
                 ces[i][j].clour=3;
                 ces[i][j].y=((ts[0]-'0')*10+(ts[1]-'0'))*10+(ts[2]-'0');
                 ces[i][j].x=-1;
            }
            else                          //都要
            {
                 ces[i][j].clour=4;
                 ces[i][j].y=((ts[0]-'0')*10+(ts[1]-'0'))*10+(ts[2]-'0');
                 ces[i][j].x=((ts[4]-'0')*10+(ts[5]-'0'))*10+(ts[6]-'0');
            }
        }
      for(int i=0;i<n;i++)
      for(int j=0;j<m;j++)
       {
           //cout<<ces[i][j].clour<<endl;
         //  cout<<i*m+j<<" ";
       }


    for(int i=0;i<n;i++)
      for(int j=0;j<m;j++)
      {
          int counts=0;
          if(ces[i][j].clour==2) //横向的
          {
              for(int k=j+1;k<m;k++)
              {
                  if(ces[i][k].clour!=5)break;
                  adde(i*m+j,i*m+k,8);
                  counts++;
              }
              adde(ss,i*m+j,ces[i][j].x-counts);
          }
          else if(ces[i][j].clour==3)   //纵向的
         {
              for(int k=i+1;k<n;k++)
              {
                 if(ces[k][j].clour!=5)break;
                  adde(k*m+j,i*m+j,8);
                  counts++;
              }
              adde(i*m+j,tt,ces[i][j].y-counts);
          }
           else if(ces[i][j].clour==4)    //都要填的，一个格子要2个编号，注意。
         {

              for(int k=j+1;k<m;k++)
              {
                 if(ces[i][k].clour!=5)break;
                  adde(i*m+j,i*m+k,8);
                  counts++;
              }
              adde(ss,i*m+j,ces[i][j].x-counts);
            counts=0;
              for(int k=i+1;k<n;k++)
              {
                   if(ces[k][j].clour!=5)break;
                  adde(k*m+j,i*m+j+n*m+2,8);
                  counts++;
              }
              adde(i*m+j+n*m+2,tt,ces[i][j].y-counts);
          }
      }
     // adde(0,ss,2);
   /* for(int i=0;i<=n*m+1;i++)
      for(int j=head[i];j!=-1;j=e[j][1])
      {
          printf("%d->%d:%d\n",i,e[j][0],e[j][2]);
      }*/
}
void out()
{
    for(int i=0;i<n;i++)
      for(int j=0;j<m;j++)
      {
          if(ces[i][j].clour!=5)printf("_");
          else
          {
              int sflow=0;
              for(int k=head[i*m+j];k!=-1;k=e[k][1])      //统计的时候只要正向边（这里注意！），其实每个点也就一条出的正向边
              {
                  if(k%2==0)
                   sflow+=8-e[k][2];
              }
              printf("%d",sflow+1);
          }
          if(j==m-1)printf("\n");
          else printf(" ");
      }
}
void init()
{
    nume=0;
    memset(head,-1,sizeof(head));
    ss=n*m;tt=n*m+1;
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        init();
        read_build();
        dinic();
        out();
    }
    return 0;
}

hdu3338 / 方格横纵和问题终极版，最大流斩,布布扣,bubuko.com

hdu3338 / 方格横纵和问题终极版，最大流斩

原文：http://blog.csdn.net/u011498819/article/details/38488167