原始Kmeans原理:
Kmeans为无监督学习(即样本无标签,简单理解为没有Y值,只有X)
Kmeans将给定的样本分为k个类,每一类成为一簇(clustering),目标是让每一簇样本紧密联系,簇与簇之间间隔较大
数学公式表示:
假设样本分$(C_{1},C_{2},,C_{k})$,则优化目标为最小化平方误差E:
$E=\frac{\left \| x-\mu _{i} \right \|_{2}^{2}}{K}$
其中$\mu _{i}$是簇Ci的均值向量,or质心。
$\mu _{i}=\frac{1}{\left | C_{i} \right |}\underset{x\subseteq C_{i}}{\sum } x$
但是上述优化目标难以实现,成为NP完全问题,只能采用启发式迭代。
tips:
插几个概念:
闵可夫斯基(Minkowski)距离:
$\sqrt[p]{\left | x-\mu _{i} \right |^{p}}$
当p=2时,为欧氏距离,也即是上文使用的$\left \| x-\mu _{i} \right \|_{2}$
当p=1时,为曼哈顿距离。
NP完全问题:
简单理解为生成一个问题的解比验证一个问题的解难得多。举例:在一个超级大的party上,你想知道是否里面有熟人,你需要将每个人都辨认一遍,很难
但是有人告诉你餐桌前拿着香槟,黄色连衣裙,正在捂嘴笑的女士你认识,那么你只需看一眼这位女士即可。
启发式迭代:网上解释的差强人意,各种百度词条和wiki。结合例子理解:
Kmeans求解过程,随机或根据经验给出k个初始点,简单起见,k=3,
第一步:计算所有样本到这三个点(A,B,C)的距离,将样本到点A距离最小,划为A类;到B距离最小,划为B...
第二步:现在有三类样本,计算各自的质心,A‘,B‘,C‘,重复上述两步骤。
如图
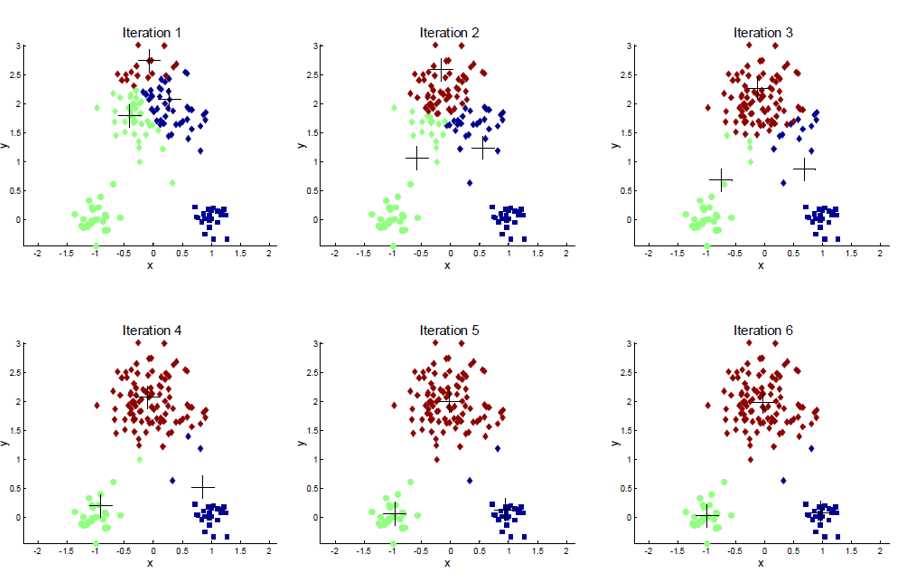
但是启发式迭代有弊端,可能不是全局最优(optimal)
(from wiki A heuristic technique (/hj???r?st?k/; Ancient Greek: ε?ρ?σκω, “find” or “discover”), often called simply a heuristic, is any approach to problem solving, learning, or discovery that employs a practical method, not guaranteed to be optimal, perfect, logical, or rational, but instead sufficient for reaching an immediate goal. Where finding an optimal solution is impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution.)
当初始点(initial)给的不好会出现下图情况:
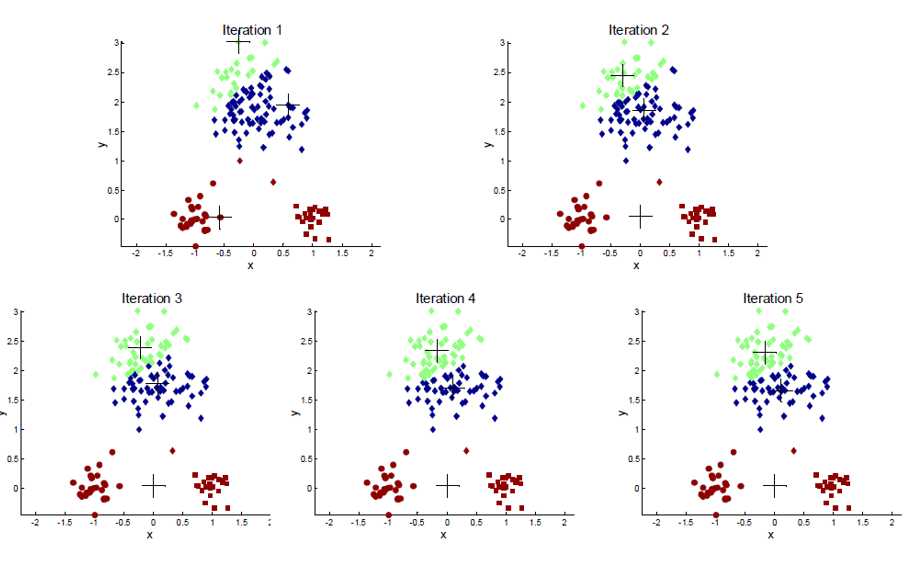
原始Kmeans的pros and cons
优点:
原理简单,收敛速度快,参数少
缺点:
K值选取难,局部最优,噪点离群点影响大,只适合样本超球体或不适合non-convex shapes,比如经典的下图:
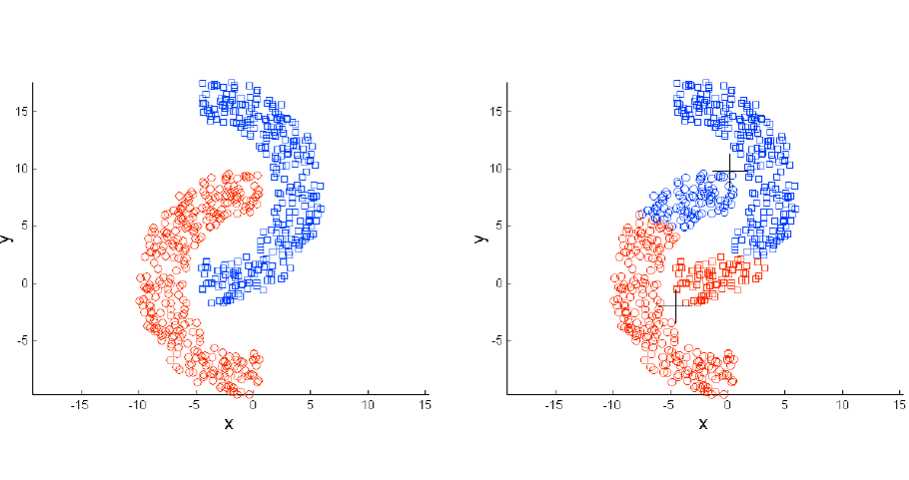
原文:https://www.cnblogs.com/super-yb/p/10861181.html