第一篇博客,浅谈自己对高斯过程和贝叶斯优化的理解,有误处欢迎指正。
一. 高斯过程回归
1. 高斯过程到底是个什么东西?!
简单来说,高斯过程可以看成是一个函数,函数的输入是x,函数的输出是高斯分布的均值和方差。
对于一些X值有对应的Y值,从X到Y存在映射关系f,即f(X)=Y,这里我们假设所有的Y是服从正态分布的!而高斯过程可以拟合出这个函数f的分布。
下图1中的两个黑点是我们已知的二维平面上的(x,y)对,我们需要通过这些点去拟合、评估、估计、猜测X与Y间真实的映射关系,通过不同的构造方法我们可以得到无数种不同的可能性。前文提到Y服从正太分布,可以这样理解:在X取某一值的时候,根据拟合的函数不同可以得到不同的Y值,但是这些不同的Y是服从正太分布的,亦如图2所示。所以高斯过程得到的是Y的分布,而非具体的Y值,Y的方差觉得了图2中阴影的宽度(y轴方向)。随着已知(x,y)对的增加,阴影面积会减小,即方差变小,函数f结构会越来越确定。
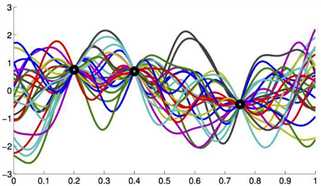
图1
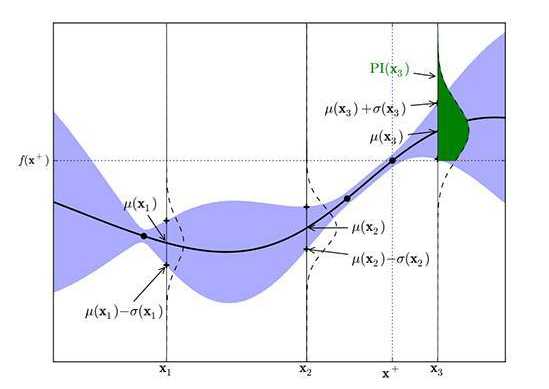
图2
2. 联合正太分布
高斯过程通过假设Y值服从联合正态分布,来考虑yn和yn+1之间的关系,因此需要给定参数包括:均值向量和协方差矩阵,即:
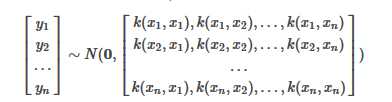
其中协方差矩阵又叫做 核矩阵, 记为K,仅和特征x有关,和y无关。
高斯过程的思想是: 假设Y服从高维正态分布(先验),而根据训练集可以得到最优的核矩阵 ,从而得到后验以估计测试集Y*,我们有后验:
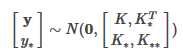
其中:
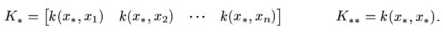
有了联合分布接下来就可以比较容易的求出预测数据y*的条件分布p(y*|y)了,经过推导其条件分布也服务高斯分布,如下:
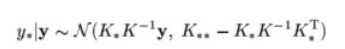
对y*估计,则可使用均值作为其估计值,即
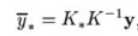
3. 为什么要使用核函数
上文提到假设Y值服从联合正态分布,需要给定参数包括:均值向量和协方差矩阵,这里我们先回顾一下什么是协方差矩阵,以及为什么可以用核矩阵代替协方差矩阵。
首先协方差矩阵的相关定义如下:

补充:相关系数和协方差的关系。

引入核函数的目的是为了拟合的函数更加光滑,在计算协方差时,我们先0均值化,可发现其就是两个向量内积的形式,由此我们可以联想到支持向量机中对核函数的使用,
核函数在低维计算的结果可以完全等价于两个变量高维映射后的内积,如图4,在低位拟合得到的曲线是不光滑的,若增加维数肯定可以使拟合曲线更加光滑。这个过程可以拆分为X1和X2求内积,转化到先将X1和X2映射到高维后再求内积,而核函数的使用可以直接取代这个过程,且可以映射到无限高的维度上。
图4
二. 贝叶斯优化
贝叶斯优化用于机器学习调参由J. Snoek(2012)提出,主要思想是,给定优化的目标函数(广义的函数,只需指定输入和输出即可,无需知道内部结构以及数学性质),通过不断地添加样本点来更新目标函数的后验分布(高斯过程,直到后验分布基本贴合于真实分布。简单的说,就是考虑了上一次参数的信息**,从而更好的调整当前的参数。
他与常规的网格搜索或者随机搜索的区别是:
贝叶斯优化是基于数据使用贝叶斯定理估计目标函数的后验分布,然后再根据分布选择下一个采样的超参数组合。它充分利用了前一个采样点的信息,其优化的工作方式是通过对目标函数形状的学习,并找到使结果向全局最大提升的参数
高斯过程 用于在贝叶斯优化中对目标函数建模,得到其后验分布
通过高斯过程建模之后,我们尝试抽样进行样本计算,而贝叶斯优化很容易在局部最优解上不断采样,这就涉及到了开发和探索之间的权衡。
而如何高效的采样,即开发和探索,我们需要用到 Acquisition Function, 它是用来寻找下一个 x 的函数。
探测(exploration)就是在还未取样的区域获取采样点。开发(exploitation)就是根据后验分布,在最可能出现全局最优解的区域进行采样。我们下一个选取点(x)应该有比较大的均值(开发)和比较高的方差(探索)。
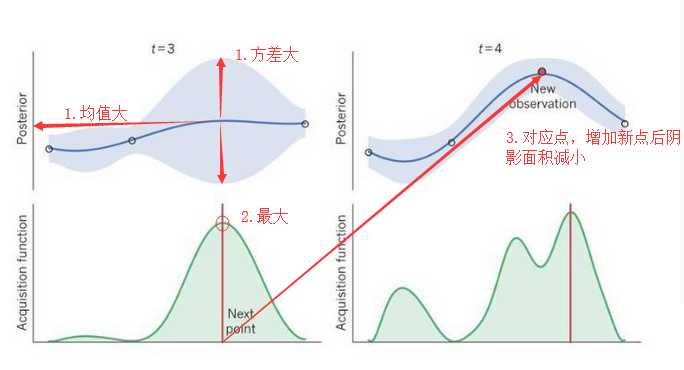
图5
使用不同的采集函数对比如下:
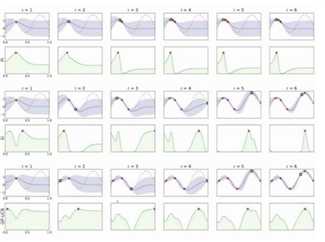
图6
贝叶斯优化过程
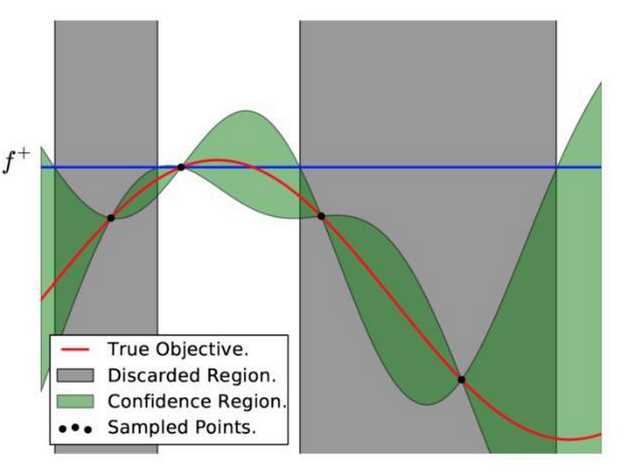
图7
上图可以直观地解释贝叶斯优化。其中红色的曲线为实际的目标函数,并且我们并不知道该函数确切的表达式。所以我们希望使用高斯过程逼近该目标函数。通过采样点(上图有 4 个抽样点),我们能够得出直观或置信曲线以拟合观察到的样本点。所以上图绿色的区域为置信域,即目标曲线最有可能处于的区域。从上面的先验知识中,我们确定了第二个点(f+)为最大的样本观察值,所以下一个最大点应该要比它大或至少与之相等。因此,我们绘制出一条蓝线,并且下一个最大点应该位于这一条蓝线之上。因此,下一个采样在交叉点 f+和置信域之间,我们能假定在 f+点以下的样本是可以丢弃的,因为我们只需要搜索令目标函数取极大值的参数。所以现在我们就缩小了观察区域,我们会迭代这一过程,直到搜索到最优解。
原文:https://www.cnblogs.com/mmqm18/p/10863088.html