动态规划

算法思想

将待求解的问题分解为若干个子问题，按顺序求解子问题，同时前一子问题的解，为后一子问题的求解提供了有用的信息。

算法优点

针对每一个状态只需要进行一次运算，之后就可以重复利用这个状态的值，从而减少了大量不必要的重复计算。也就是，一旦出现重复的子问题求解，优先考虑动态规划方式求解，一般都会获得很多优化

算法特点

• 求解子问题时只保存针对当前子问题的最优解
• 重叠子问题，减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个数组中。
• 子问题往往不是互相独立的

动态规划条件

• 总问题可划分为多个子问题
• 通过子问题的最优解可以获得整个问题的最终最优解
• 子问题必须具有无后效性。当前状态的子问题的解不会被之后状态的子问题影响
• 动态规划的子问题不独立，单个子问题的最优解可以使用之前已解决的子问题的解，这也是动态规划的优点

求解步骤

• 子问题的划分。 按照一定的顺序把整个问题划分为若干个规模相等的子问题
• 子问题状态的确定。根据问题需求和子问题的各个属性确定子问题的”状态“，同时需要满足无后效性。
• 推导状态转移方程。 状态转移指的就是根据上一个状态（或者叫上一个子问题的解）来获取当前子问题解的过程
• 边界条件和初始值的确定。由于动态规划是根据之前子问题的解来推导当前子问题的解，所以最初状态的值必须确定。边界条件是用来描述结束状态的，如果当前状态完全到达边界，便视为已经到达了最终状态。

算法实例

问题1：斐波那契数列

数列由1，1开始，之后的斐波那契数列系数就由之前的两数相加。

Sequence： 1，1，2，3，5，8，13，21，34，……

状态转移方程：

问题2：收益最大

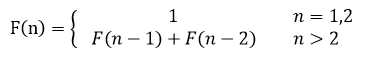
纵轴是所作的任务，以及收益；横轴是对应任务所对应的时间。选取规则为时间不能重叠，使得收益最大。

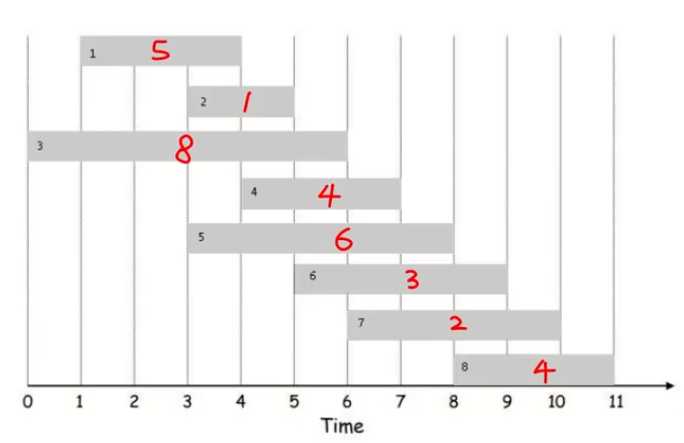
任务编号：       1，2，3，4，5，6，7，8

任务对应收益v(i)：5，1，8，4，6，3，2，4

第i个任务选状态（选和不选）最优解opt(i)：

pre(i)为之前的状态，对应任务编号的先前状态表：

i:       1  2  3  4  5  6  7   8             
pre(i):  0  0  0  1  0  2  3   5               
opt(i):  5  5  8  9  9  9  10  13 

问题3：不相邻元素总和最大

给定一个数组，选取一些元素使得总和最大，选取规则为不能连续取两个元素，即选取的元素之间至少要间隔一个其它元素，每个元素都有选与不选两种可能，使得用动态规划求解。

arr： 1，2，4，1，7，8，3

状态转移方程

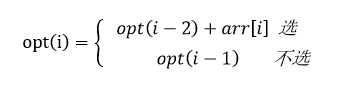
出口条件

opt[0] = arr[0]             
opt[1] = max(arr[0], arr[1])

问题4：寻找和为定值的数

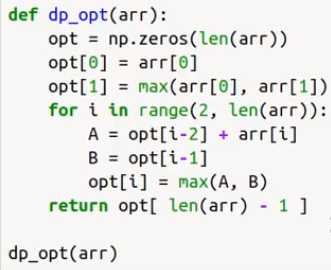
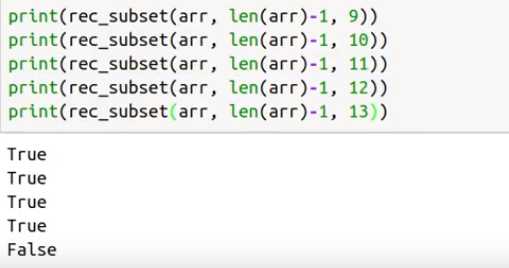
给定一个数组，选取一些元素使得总和为给定的值。

arr：  3，34，4，12，5，2
s：    9

subset(arr, i, s)：数组arr当前第i个数字需要计算的和为s

状态转移方程

if s = =0:                              
    return true                             
elif i == 0:                                    
    return arr[0] == s                         
elif arr[i] > s:                           
    return subset(arr, i-1, s)   

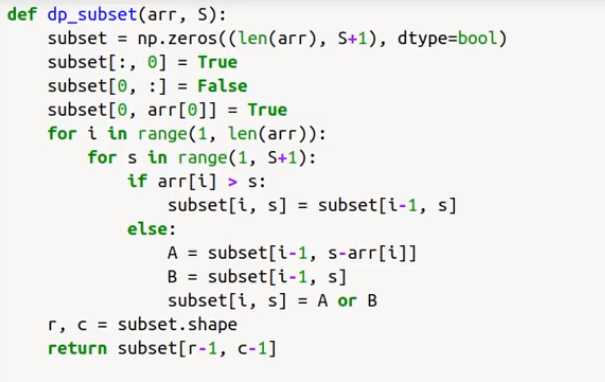
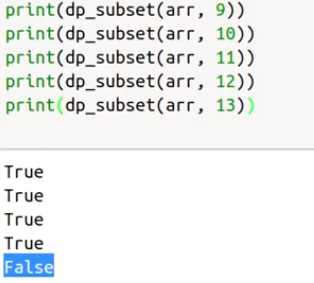
使用二维数组进行存储结果

arr   i    0  1  2  3  4  5  6  7  8  9        s          
3     0    F  F  F  F  F  F  F  F  F  F                               
34    1    T                                               
4     2    T                                                    
12    3    T                                                       
5     4    T                                                      
2     5    T                                                  

动态规划

原文：https://www.cnblogs.com/yusq77/p/10862592.html