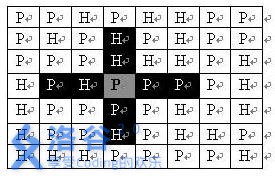
此题意思很简单,如下图,就是十字架上的不能有两个点放炮兵。
分析:
而m即一行的个数小于等于10,每个格子上只有防或不放两种情况
很自然就会想到状压DP
还有一点很重要:
要符合题目条件的 只有平原可以放炮兵。
所以还要匹配 炮兵放法与平原 的关系(一共要判断3种,PH,列列列,横横横)。
如下是DP思考过程:(和玉米田差不多)
我们需要考虑定义,我们可以定义dp[i][j][k]表示到第i行状态为j,且上一行状态为k时的最大方案数
然后我们要来考虑初始化,因为状态肯定由前两行推过来,所以我们需要单独处理第一二行的方案数
取最大的话就一定要和 原来的自己、前一个状态+增长 比较,取较大的那个
最后还有一个问题,数组dp[105][1024][1024]!!!!这空间超400MB啊!
所以还得优化空间。
滚动数组:因为当前状态只与前两行有关,所以只需保留有用的三行
dp[105][1024][1024] --> dp[3][1024][1024] 好很多了(已经不爆了,但我们要做到最优,这是OIer的信念)
预处理:实际上没有几种情况是可以满足横排的(m = 10时,70个不到),于是我们就可以把这些满足条件的保存下来。~~~
dp[3][1024][1024] --> dp[3][70][70]
代码:
#include<cstdio> #include<iostream> using namespace std; const int maxn=101; int n,m; int st[70],sum[70]; int cnt; int dp[3][70][70]; int map[maxn]; int ans=0; void init(int s,int tot,int i) { if(i>=m) { st[++cnt]=s; sum[cnt]=tot; //printf("st=%d sum=%d\n",st[cnt],sum[cnt]); return; } init(s,tot,i+1); init(s+(1<<i),tot+1,i+3); } void add() { for(int i=1;i<=cnt;i++) { //printf("st=%d map=%d ",st[i],map[0]); if(!(map[1]&st[i])) { dp[1][i][0]=sum[i]; //printf("%d\n",dp[1][i][0]); } //printf("sum=%d %d\n",sum[i],dp[0][i][0]); } for (int i=1;i<=cnt;i++) { if(!(st[i]&map[2])) for (int j=1;j<=cnt;j++) if((!(st[j]&map[1]))&&(!(st[i]&st[j]))) { dp[2][i][j]=sum[i]+sum[j]; //printf("i=%d j=%d %d\n",st[i],st[j],dp[2][i][j]); } } } void come_dp() { for (int i=3;i<=n;i++) { for (int j=1;j<=cnt;j++) { if(!(st[j]&map[i])) for (int k=1;k<=cnt;k++) if((!(st[k]&map[i-1]))&&(!(st[k]&st[j]))) { for (int u=1;u<=cnt;u++) if((!(st[u]&map[i-2]))&&(!(st[u]&st[j]))&&(!(st[u]&st[k]))) dp[i%3][j][k]=max(dp[i%3][j][k],dp[(i-1)%3][k][u]+sum[j]); } } } } void work() { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) { for (int j=1;j<=m;j++) { char x; cin>>x; map[i]<<=1; if(x==‘H‘) map[i]+=1; } } //printf("%d\n",map[1]); init(0,0,0); add(); come_dp(); for (int i=1;i<=cnt;i++) for (int j=1;j<=cnt;j++) ans=max(ans,dp[n%3][i][j]); printf("%d",ans); } int main() { work(); return 0; }
逃qaq
原文:https://www.cnblogs.com/mzyczly/p/10886670.html