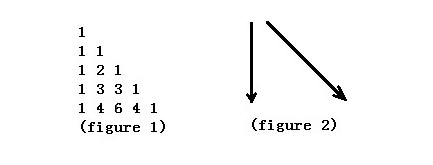
1 1 2 4 2 7
Case #1: 0 Case #2: 5
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
int n,m,p;
const int maxn = 10000+10;
bool isPrime[maxn];
int CC[maxn][maxn];
int AA[maxn][maxn];
void gcd(int a,int b,int &d,int &x,int &y){
if(!b){
d = a;
x = 1;
y = 0;
}else{
gcd(b,a%b,d,y,x);
y -= x*(a/b);
}
}
inline int inv(int a,int p){
int d,x,y;
gcd(a,p,d,x,y);
return (d==1)?(x+p)%p:-1;
}
inline int C(int nn,int mm){
int ans;
if(nn<mm) return 0;
if(nn==mm||mm==0) return 1;
if(mm==1||mm==nn-1) return nn;
ans = (((AA[p][nn]*CC[p][mm])%p)*CC[p][nn-mm])%p;
return ans;
}
int Lucas(int nn,int mm){
if(mm==0) return 1;
int k = C(nn%p,mm%p);
return (k*Lucas(nn/p,mm/p))%p;
}
void init(){
memset(isPrime,1,sizeof isPrime);
int id = 0;
for(int i = 2; i < maxn; i++){
if(isPrime[i]){
CC[i][2] = inv(2,i);
for(int j = 3; j < i; j++){
CC[i][j] = (CC[i][j-1]*inv(j,i))%i;
}
for(int j = i*i; j < maxn; j+=i){
isPrime[j] = 0;
}
AA[i][1] = 1;
for(int j = 2; j < i; j++){
AA[i][j] = (AA[i][j-1]*j)%i;
}
}
}
}
int main(){
int T = 1;
init();
while(scanf("%d%d%d",&n,&m,&p) != EOF){
if(2*m < n)
printf("Case #%d: %d\n",T++,(Lucas(n+1,m)+n-m)%p);
else
printf("Case #%d: %d\n",T++,(Lucas(n+1,m+1)+m)%p);
}
return 0;
}
HDU3944-DP?(帕斯卡公式+Lucas定理),布布扣,bubuko.com
原文:http://blog.csdn.net/mowayao/article/details/38493489