扩展KMP笔记

KMP能计算一个字符串的每个位置前最长公共前缀后缀

扩展KMP可以用来计算两个字符串间的最长公共前缀后缀的……

不过为了计算这个需要绕些弯路

已知字符串$S$和$P$，$S$的长度为$n$，$P$的长度为$m$

扩展KMP实际是计算$E$数组，设$E[i]$为字符串$S[i..n-1]$与字符串$P$的最大公共前缀

尝试数学归纳法

$E[0]$显然只能直接依次比对，因为什么信息都没有

假设$E[0]\sim E[i-1]$都计算出来了，现在计算$E[i]$

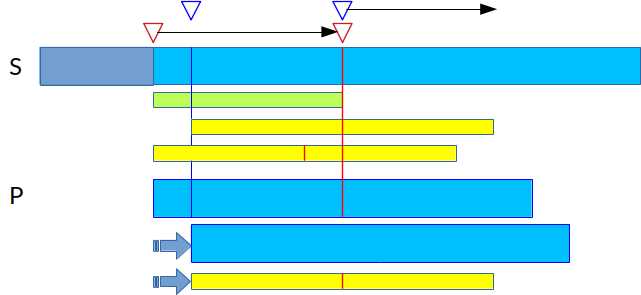
不妨= =，利用$E[i-1]$的信息，第二行的矩形的宽度表示$E[i-1]$，只有这个信息是不够的，否则计算$E[i]$还是需要重复跑计算$E[i-1]$跑过的距离

假设有“$P[i..m-1]$与$P$的最大公共前缀长度”的信息，设为$N[i]$

• 如果$i+N[1]>(i-1)+E[i-1]$，由于红线右边的P与S是否相等不确定，因此要舍去红线右边的部分，那么经过如图的变形（第三排和第四排的矩形），可以直接从上一次失败的地方继续（红线处）
• 如果$i+N[1]\leqslant(i-1)+E[i-1]$，那么直接就可以得到$E[i]=N[1]$

由于第一种情况中仍然可能重复对比$S$和$P$，$E[i-1]$可能不是最好的选择，那么我们就选红线最靠右的$E[k]$来计算$E[i]$

• 如果$i+N[i-k]>k+E[k]$，由于红线右边的P与S是否相等不确定，因此要舍去红线右边的部分，那么经过如图的变形（第三排和第四排的矩形），可以直接从上一次失败的地方继续（红线处）
• 如果$i+N[i-k]\leqslant k+E[k]$，那么直接就可以得到$E[i]=N[i]$

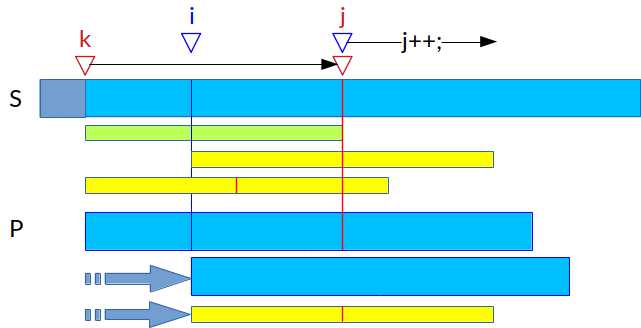
这样，在知道$N[i]$的情况下，可以$\mathcal{O}(n)$得到$E$数组（因为S与P的比较不会重复）

代码：

inline void getE() {
    int j = 0;
    while(j < n && j < m && s[j] == p[j])j++;
    E[0] = j; //直接计算E[0]

    int k = 0;
    REP(i,1,n) {
        int R = E[k]+k-1;
        int L = N[i-k];
        if(i+L < R+1)E[i] = L;
        else {
            j = max(0,R-i+1);
            while( i+j < n && j < m && p[i+j] == s[j] )j++;
            E[i] = j;
            k = i; //更新红线最靠右的k
        }
    }
}

对于$N$数组，和求$E$数组类似

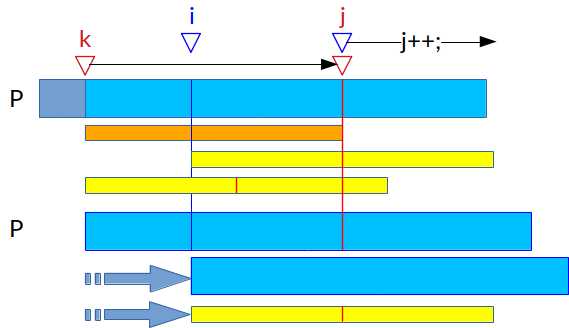
$N[0]=m$，$N[1]$直接计算，假设$N[0]\sim N[i-1]$都求出来了，选红线最靠右的$N[k]$，那么

• 如果$i+N[i-k]>k+N[k]$，那么直接从上一次失败的地方继续（红线处）
• 如果$i+N[i-k]\leqslant k+N[k]$，那么$N[i]=N[i-k]$

代码：

inline void getN() {
    N[0] = m;

    int j = 0;
    while( j+1 < m && p[j] == p[j+1] )j++;
    N[1] = j;

    int k = 1;
    REP(i,2,m) {
        int R = N[k]+k-1;
        int L = N[i-k];
        if( i+L < p+1 )N[i] = L;
        else {
            j = max(0,R-i+1);
            while( i+j < m && x[i+j] == x[j])j++;
            N[i] = j;
            k = i;
        }
    }
}

 暂坑

扩展KMP笔记

原文：https://www.cnblogs.com/sahdsg/p/10887787.html