gabor滤波器

https://blog.csdn.net/u013709270/article/details/49642397

https://github.com/xuewenyuan/Gabor_Visualization

https://blog.csdn.net/u013709270/article/details/49642397

二、Gabor函数

Gabor变换属于加窗傅立叶变换，Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。另外Gabor函数与人眼的生物作用相仿，所以经常用作纹理识别上，并取得了较好的效果。二维Gabor函数可以表示为：

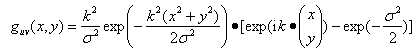
其中：

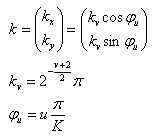
v的取值决定了Gabor滤波的波长，u的取值表示Gabor核函数的方向，K表示总的方向数。参数决定了高斯窗口的大小，这里取。程序中取4个频率（v=0, 1, ..., 3），8个方向（即K=8，u＝0, 1, ... ,7），共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示：

图片来源：GaborFilter.html

图片来源：http://www.bmva.ac.uk/bmvc/1997/papers/033/node2.html

三、代码实现

Gabor函数是复值函数，因此在运算过程中要分别计算其实部和虚部。代码如下：

private void CalculateKernel(int Orientation, int Frequency)
{
   double real, img;
   for(int x = -(GaborWidth-1)/2; x<(GaborWidth-1)/2+1; x++)
      for(int y = -(GaborHeight-1)/2; y<(GaborHeight-1)/2+1; y++)
      {
         real = KernelRealPart(x, y, Orientation, Frequency);
         img = KernelImgPart(x, y, Orientation, Frequency);
         KernelFFT2[(x+(GaborWidth-1)/2) + 256 * (y+(GaborHeight-1)/2)].Re = real;
         KernelFFT2[(x+(GaborWidth-1)/2) + 256 * (y+(GaborHeight-1)/2)].Im = img;
      }
}
private double KernelRealPart(int x, int y, int Orientation, int Frequency)
{
   double U, V;
   double Sigma, Kv, Qu;
   double tmp1, tmp2;
   U = Orientation;
   V = Frequency;
   Sigma = 2 * Math.PI * Math.PI;
   Kv = Math.PI * Math.Exp((-(V+2)/2)*Math.Log(2, Math.E));
   Qu = U * Math.PI  / 8;
   tmp1 = Math.Exp(-(Kv * Kv * ( x*x + y*y)/(2 * Sigma)));
   tmp2 = Math.Cos(Kv * Math.Cos(Qu) * x + Kv * Math.Sin(Qu) * y) - Math.Exp(-(Sigma/2));
   return tmp1 * tmp2 * Kv * Kv / Sigma;   
}
private double KernelImgPart(int x, int y, int Orientation, int Frequency)
{
   double U, V;
   double Sigma, Kv, Qu;
   double tmp1, tmp2;
   U = Orientation;
   V = Frequency;
   Sigma = 2 * Math.PI * Math.PI;
   Kv = Math.PI * Math.Exp((-(V+2)/2)*Math.Log(2, Math.E));
   Qu = U * Math.PI  / 8;
   tmp1 = Math.Exp(-(Kv * Kv * ( x*x + y*y)/(2 * Sigma)));
   tmp2 = Math.Sin(Kv * Math.Cos(Qu) * x + Kv * Math.Sin(Qu) * y) - Math.Exp(-(Sigma/2));
   return tmp1 * tmp2 * Kv * Kv / Sigma;   
}

有了Gabor核函数后就可以采用前文中提到的“离散二维叠加和卷积”或“快速傅立叶变换卷积”的方法求解Gabor变换，并对变换结果求均值和方差作为提取的特征。32个Gabor核函数对应32次变换可以提取64个特征（包括均值和方差）。由于整个变换过程代码比较复杂，这里仅提供测试代码供下载。该代码仅计算了一个101×101尺寸的Gabor函数变换，得到均值和方差。代码采用两种卷积计算方式，从结果中可以看出，快速傅立叶变换卷积的效率是离散二维叠加和卷积的近50倍。

代码下载请点 >>>>  这里 。注意，代码中没有包含Exocortex.DSP，请测试者到相应网站上下载并包含在自己的项目中。

解压缩后，里面有一"GaborTest.png"文件，程序中默认路径是“D:\”，请将此图片放置到此路径下。（程序代码在Visual Studio .net 2003下调试通过）。

gabor滤波器

原文：https://www.cnblogs.com/shuimuqingyang/p/10889035.html