(前面都是废话)
下面是Dijkstra人物生平(摘自百度百科):
艾兹格·W·迪科斯彻 (Edsger Wybe Dijkstra,1930年5月11日~2002年8月6日)荷兰人。 计算机科学家,毕业就职于荷兰Leiden大学,早年钻研物理及数学,而后转为计算学。曾在1972年获得过素有计算机科学界的诺贝尔奖之称的图灵奖,之后,他还获得过1974年 AFIPS Harry Goode Memorial Award、1989年ACM SIGCSE计算机科学教育教学杰出贡献奖、以及2002年ACM PODC最具影响力论文奖。[1]
(说实话,这种东西看都不用看,要不是为了凑字数我也不会放上2333)
下面是算法讲解部分
1、最短路问题(有基础可以直接跳至小标题2)
所谓最短路问题,即在一个图中,求一点到达任意一点的最短距离,如图1
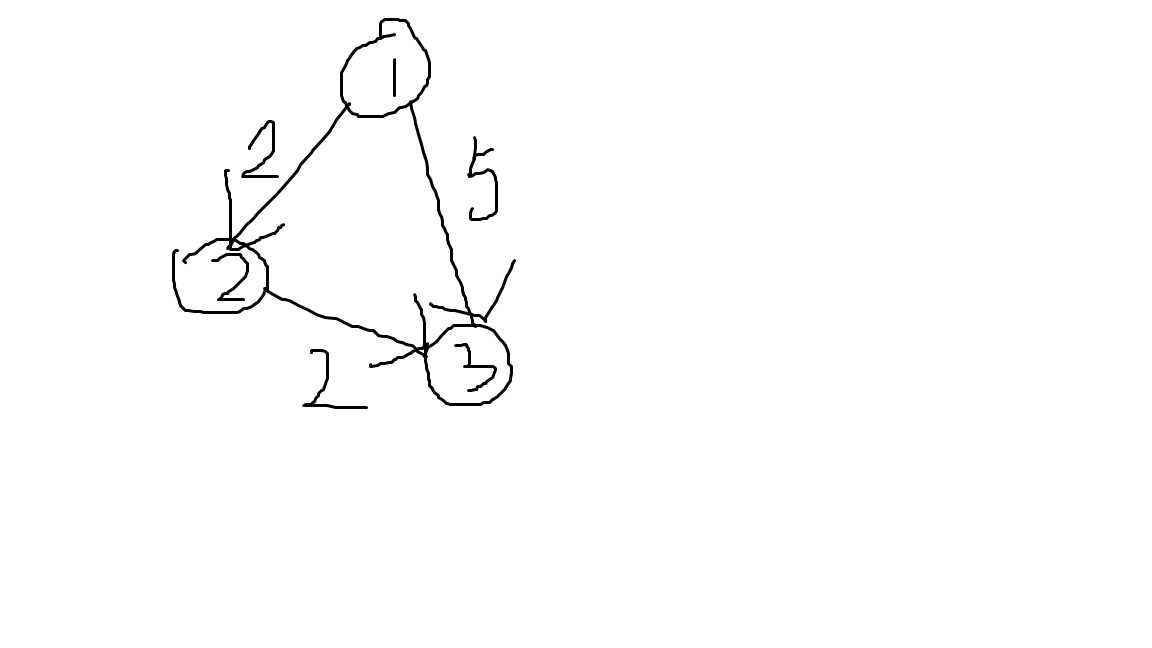
如图,这是一个有向图(图中每条边只能从其一个端点a走向另一个端点b,而不能从b走向a,相反地,无向图中的边既可以从a走向b也可以从b走向a)图中的圆圈即我们通常说的“顶点”,两个顶点之间的线就是我们所说的“边”,圆圈中的数即这个顶点的编号,边旁边的数即“权值”(可以理解为边的长度)
现在我们想求顶点1到顶点3的最短路(即使一个顶点到达另一个顶点所走的边的权值之和最小),显然有两种走法:
一种是1->3,另一种是1->2->3
很容易看出,1->2->3这种走法所经过的边的权值之和最小,即顶点1到顶点3的最短路
那么你可能会想了,要怎么使计算机像你一样求出最短路呢?这就引出了本文的主题——Dijkstra算法
2、Dijkstra算法
算法简介:
Dijkstra算法是由荷兰神犇Dijkstra发明的最短路算法,是目前最快的寻路算法,堆优化后时间复杂度可达O((m+n)logm),但缺点是不能处理负权边。
负权边是什么:负权边,即权值为负的边,如果用边是长度的比喻有点难理解,下面我用一下rqy神仙的比喻:
每一条边的权值可以认为是从其一端a到另一端b的过路费,而负权就是有土豪在地上撒钱,不但没有过路费还会让你花的总钱数变少
是不是很生动形象(手动滑稽)
算法思想:
Dijkstra算法的思想就是每一次选择一条未被选择的且权值最小的边连入最短路中,并用新连入的边的去松弛(即假设有三点a,b,c,a到c有一条边权值为10,但由a出发经过b再到c所经过的边的权值之和为5,那么我们就把a到c的最短路值修改为5)所有其起始端顶点的子节点,其实就是一种贪心
显然地,我们假设顶点数为n,边数为m,则此算法的时间复杂度为O(n^2),这显然是远远不够的。于是,堆优化的Dijkstra算法诞生了
3、堆优化Dijkstra算法
堆优化Dijkstra算法,即运用堆排序来加快找边的速度,使算法总体时间复杂度达到O((n+m)logm)
总的来说,就是把图中所有边都压入一个最小堆(即根节点的值最小的堆)中,每次可以直接取堆顶元素入最短路,取边的时间复杂度为O(1),但维护最小堆的时间复杂度为O(log m)
(下面是C++代码实现,我用C++自带的STL库中的优先队列模拟最小堆)
#include<bits/stdc++.h>
#define inf 0x7ffffff
using namespace std;
int n;
struct node{
int x,dis;
bool operator<(const node&a)const{
return dis>a.dis;
}
};
vector<int>son[2505],v[2505];
void make(int from,int to,int key){
son[from].push_back(to);
v[from].push_back(key);
}
#define to son[rt.x][i]
int dis[2505],tim[2505];
bool vis[2505];
priority_queue<node>q;
void dijkstra(int s){
for(int i=1;i<=n;i++){
dis[i]=inf;
}
dis[s]=0;
q.push((node){s,0});
while(!q.empty()){
node rt=q.top();
q.pop();
if(!vis[rt.x]){
vis[rt.x]=1;
for(int i=0;i<son[rt.x].size();i++){
if(dis[to]>dis[rt.x]+v[rt.x][i]){
dis[to]=dis[rt.x]+v[rt.x][i];
q.push((node){to,dis[to]});
}
}
}
}
}
int main(){
int m,s,z;
scanf("%d%d%d%d",&n,&m,&s,&z);
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
make(x,y,z);
make(y,x,z);
}
dijkstra(s);
printf("%d",dis[z]);
return 0;
}
(C++神教万岁!)
题目:洛谷P1339热浪
4、斐波那契堆优化的Dijkstra
使用斐波那契堆可以使Dijkstra算法的时间复杂度进一步优化,这个坑以后再填。
(我才不会说是我还不会呢哼)
引用:
原文:https://www.cnblogs.com/Wahearer/p/10891066.html