这章学习了图,因为编程题还没做,所以这篇博客就先梳理一下这章学习的内容
1、顶点对<x,y>是有序的;(x,y)是无序的
2、使用邻接矩阵表示顶点之间的关系:
缺点:空间复杂度高,稀疏矩阵时会造成空间浪费、不便于增加和删除顶点、不便于统计边的数目
优点:可以较方便查两点间是否相连、查度多少、增加和删除顶点之间的边
3、采用邻接矩阵表示法,创建无向网(自己试着打了下)
Status CreateUDN(AMGraph &G) //G.vexnum:总顶点数;G.arcnum:总边数;MaxInt:极大值 { cin>>G.vexnum>>G.arcnum; //输入总顶点数,总边数 for(i=0;i<G.vexnum;++i) cin>>G.vexs[i]; //依次输入点的信息 for(i=0;i<G.vexnum;++i) for(j=0;j<G.vexnum;++j) G.arcs[i][j] = MaxInt; //初始化,权值都置为极大值MaxInt for(k=0;k<G.arcnum;++k) { cin>>v1>>v2>>w; i=LocateVex(G,v1);j=LocateVex(G,v2); //确定v1和v2在矩阵中的位置,既顶点数组的下标 G.arcs[i][j] = w; G.arcs[j][i] = G.arcs[i][j]; } return OK; }
4、深搜和广搜:
给出图,邻接矩阵,邻接表如下图写出广搜和深搜的顺序:
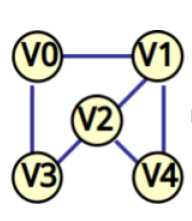
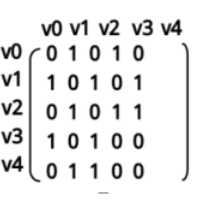
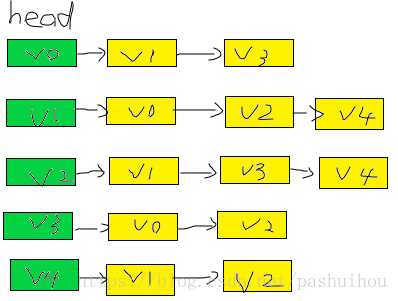
(图片转自博客https://blog.csdn.net/pashuihou/article/details/80091233)
深搜:访问顶点的第一个未被访问的邻接点,也就是每次选父节点中的一个子节点进行搜索不断下移,直到子树为空后回溯
深搜顺序:v0—v1—v2—v3—v4
广搜:每个父亲节点的子节点遍历完才遍历新的节点
顺序:v0—v1—v3—v2—v4
5、最小生成树
主要就是把初始顶点加入U中 2、选择 (最小边) 3、加入U中 4、更新(普里姆算法)
6、图的邻接表存储方式
#define MVNum 100 //最大顶点数 typedef struct ArcNode //边结点 { int adjvex; //该边所指向的顶点的位置 struct ArcNode *nextarc; //指向下一条边的指针 OtherInfo info; //和边相关的信息 } ArcNode; typedef struct VNode { VERtexType data; ArcNode *firstarc; }VNode,AdjList[MVNum]; typedef struct { ADjList vertics; int vexnum, arcnum; //图当前顶点数和边数 }SLGrapg;
总结:这周学了很多东西,但对于上周说到的提前预习和及时复习并没有很好的落实好(主要社团还有各种选修课的事都堆在这周了自己也感觉挺抱歉的)所以下周定下目标依然是做到提前预习和及时复习,而且也快期末了,希望自己接下来把更多时间放在学习上,然后也要开始准备复习一些前面学习的内容了。
原文:https://www.cnblogs.com/MRBC/p/10891552.html