好吧又被爆踩。。。暂时咕了3道。。。
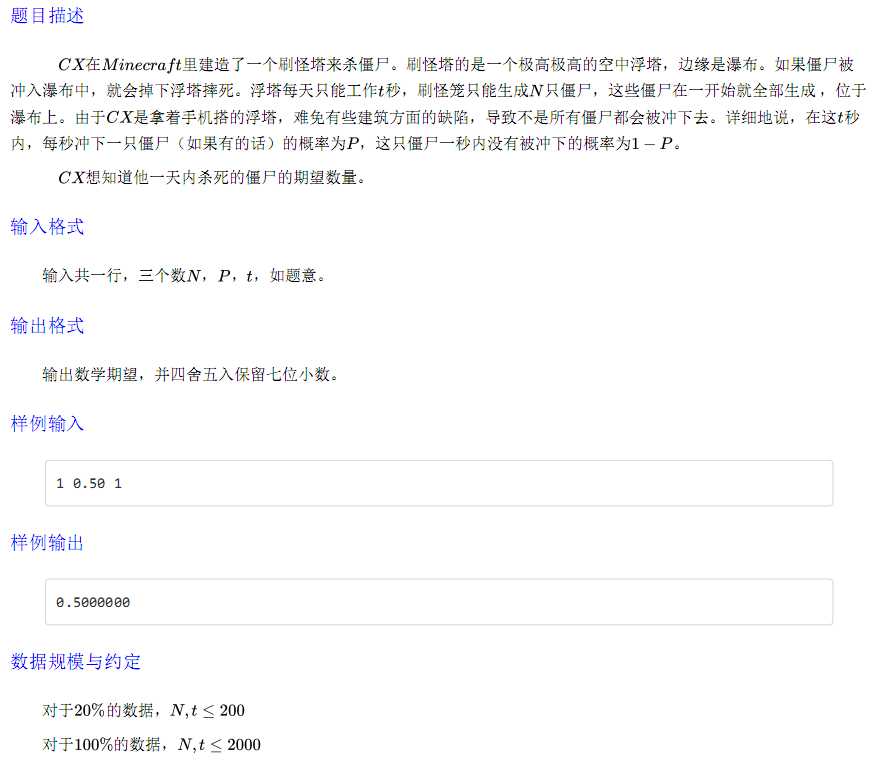
就是个简单的概率DP对吧。。可是考试时边界写挂了。。
设$ f[i][j]$表示时间为$i$时掉下$j$个僵尸的概率;
所以有
$ f[i][j]=P*f[i-1][j-1]+(1-P)*f[i-1][j] \space 当 j \neq 0 且 j \neq n $
$f[i][n]=P*f[i-1][n-1]+f[i-1][n]$
$f[i][0]=(1-P)*f[i-1][0]$
#include<cstdio> #include<iostream> #define R register #define db long double using namespace std; int n,t; db P,ans; db f[2010][2010]; signed main() { //freopen("fly.in","r",stdin); freopen("fly.out","w",stdout); scanf("%d%Lf%d",&n,&P,&t); f[0][0]=1; for(R int i=1;i<=t;++i) for(R int j=0;j<=n;++j){ if(j==n) f[i][n]=f[i-1][n]+P*f[i-1][n-1]; else if(j==0) f[i][0]=(1-P)*f[i-1][0]; else f[i][j]=f[i-1][j]*(1-P)+f[i-1][j-1]*P; } for(R int i=1;i<=n;++i) ans+=i*f[t][i]; printf("%.7Lf\n",ans); }
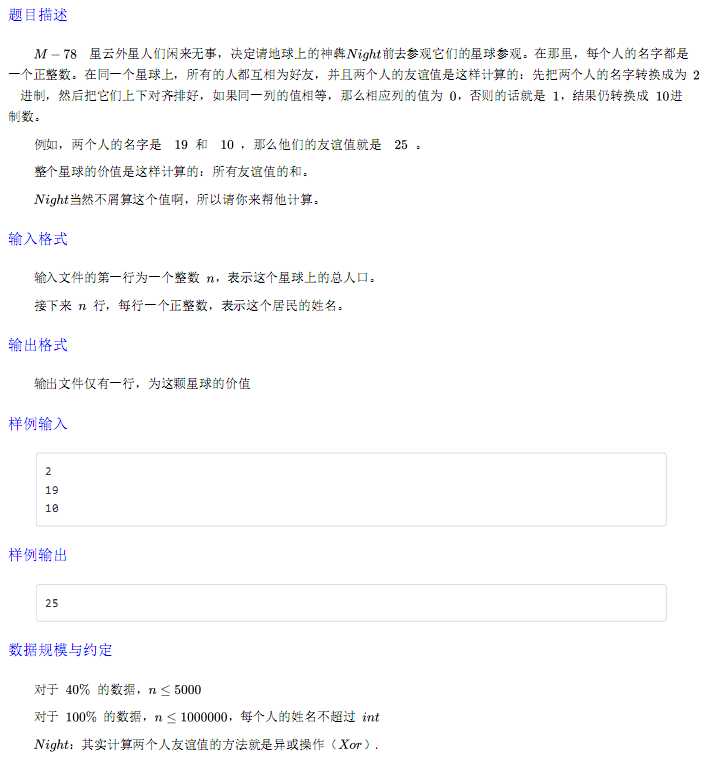
考试时没仔细想,只会$ n^2$ 暴力
$ \Sigma_{i=1}^n \Sigma_{j=1}^n a_i \space xor \space a_j =\Sigma_{k=0}^{lim} \Sigma_{i=1}^n \Sigma_{j=1}^n a_{i,k} \space xor \space a_{j,k}=\Sigma_{k=0}^{lim} \Sigma_{i=1}^n sum_{a_{i,k}==0}*sum_{a_{i,k}==1}$
#include<cstdio> #include<iostream> #define R register int using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int n,a[1000010]; long long ans; signed main() { freopen("alien.in","r",stdin); freopen("alien.out","w",stdout); n=g(); for(R i=1;i<=n;++i) a[i]=g(); register long long k=1,sum; for(R i=0;i<31;++i,k<<=1) { sum=0; for(R j=1;j<=n;++j) if(a[j]&k) ++sum; ans+=(sum*(n-sum)<<i); } printf("%lld\n",ans); }
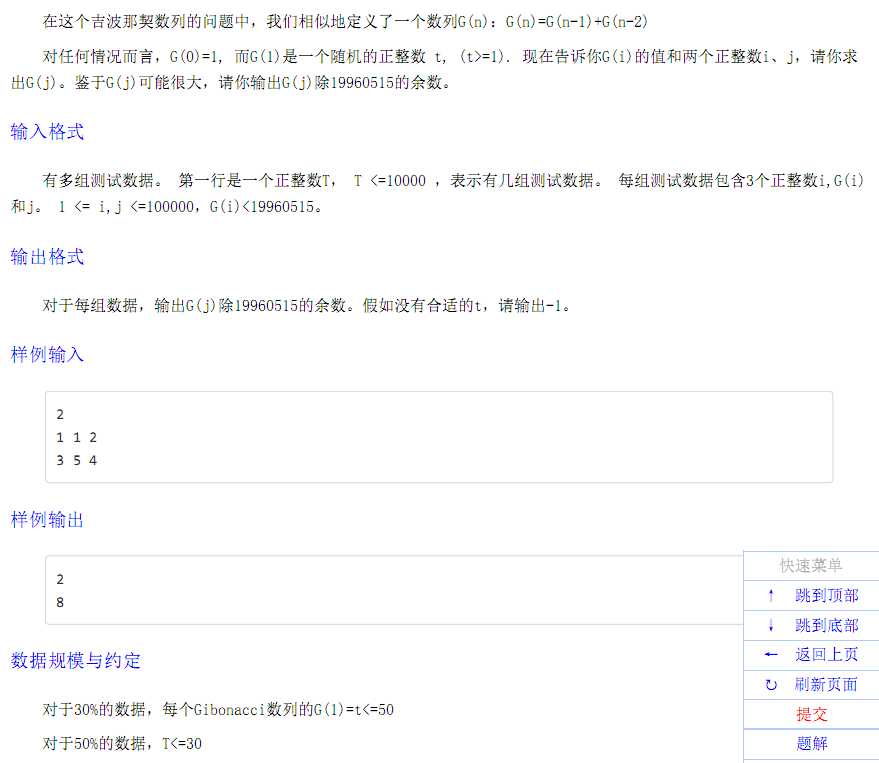
考试时没开$long long$(觉得不用开),然后就$30pts$
瞎xx推就可以
#include<cstdio> #include<iostream> #define int long long//调错专用 #define R register int using namespace std; const int mod=19960515; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int fib[100010]; int t,i,G,j; signed main() { freopen("gibonacci.in","r",stdin); freopen("gibonacci.out","w",stdout); fib[1]=1; t=g(); for(R i=2;i<=100000;++i) fib[i]=(fib[i-1]+fib[i-2])%mod; while(t--) { i=g(),G=g(),j=g(); R ran; if(i==1) ran=G,printf("%lld\n",(long long)(fib[j]*ran+fib[j-1])%mod); else { ran=(G-fib[i-1])/fib[i]; if((G-fib[i-1])%fib[i]==0) printf("%lld\n",(long long)(fib[j]*ran+fib[j-1])%mod); else printf("-1\n"); } } }
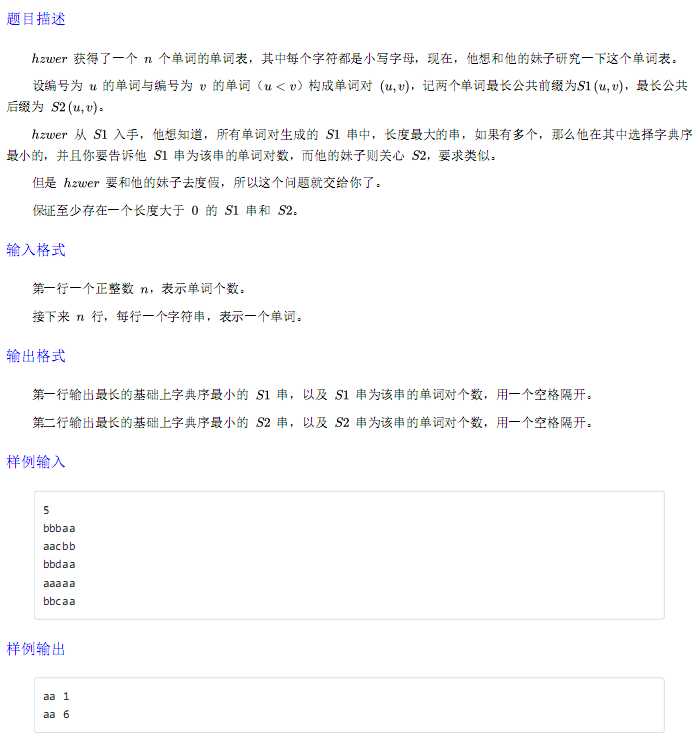

当时脑子傻了。。。拿map+string瞎干。。倒是一下就写出来了。。结果一脸震惊的望着某大佬说不就是个trie树吗。。。我怎么没想到。。。
在每一个点多维护一个sz,ins时候把每个点的sz都+1,查询时如果sz>2则说明有公共前缀(或后缀);
注意用了一个flg去处理后缀字典序最小的问题。
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #define R register int using namespace std; int n,flg,tl,num; char p[500010],ans[500010],tmp[500010]; struct node { int cnt; int tr[500010][26],sz[500010]; inline void ins(char *s) { R c,np=0; while(*s) c=*s-‘a‘,(tr[np][c]?0:tr[np][c]=++cnt),++sz[np=tr[np][c]],++s; } inline void find(int now,int dep) { for(R i=0;i<=25;++i) if(sz[tr[now][i]]>1) tmp[dep]=‘a‘+i,find(tr[now][i],dep+1); if(flg&&dep==tl) for(R p=dep-1;p>=0;--p) if(tmp[p]!=ans[p]) if(tmp[p]<ans[p]) {memcpy(ans,tmp,sizeof(char)*tl); break;} else break; if(dep>tl) tl=dep,memcpy(ans,tmp,sizeof(char)*tl),num=sz[now]; } }f,b; signed main() { freopen("wordlist.in","r",stdin); freopen("wordlist.ans","w",stdout); scanf("%d",&n); for(R i=1;i<=n;++i) scanf("%s",p),f.ins(p),reverse(p,p+strlen(p)),b.ins(p); f.find(0,0); printf("%s %d\n",ans,num*(num-1)/2); tl=0,flg=1; b.find(0,0); ans[tl]=0; reverse(ans,ans+tl); printf("%s %d\n",ans,num*(num-1)/2); }


设某个点被$D$的次数为$x$,则贡献为$x*(x+1)/2$,其实仔细想想它就是个等差数列,与第几次被$D$无关。
#include<cstdio> #include<iostream> #define R register int using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int n,m; int pre[100010],c[100010],ans[100010]; long long anss; signed main() { freopen("pony.in","r",stdin); freopen("pony.ans","w",stdout); n=g(),m=g(); for(R i=2;i<=n;++i) pre[i]=g(); for(R i=1;i<=m;++i) ++c[g()]; for(R i=1;i<=n;++i) ans[pre[i]]+=c[i],ans[i]+=c[pre[i]]+c[i]; for(R i=1;i<=n;++i) anss+=(long long)ans[i]*(ans[i]+1)/2; printf("%lld\n",anss); }
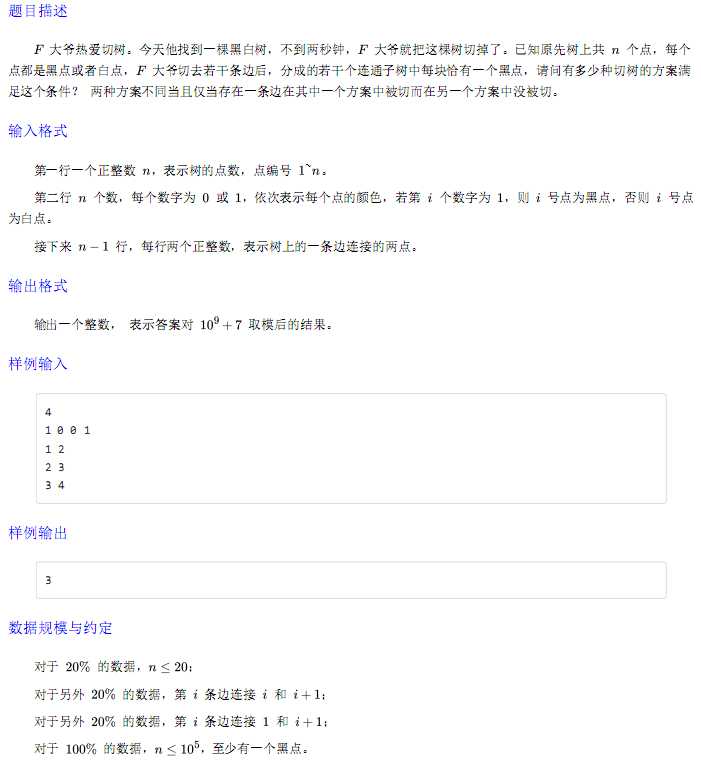
不会。。先咕着。。
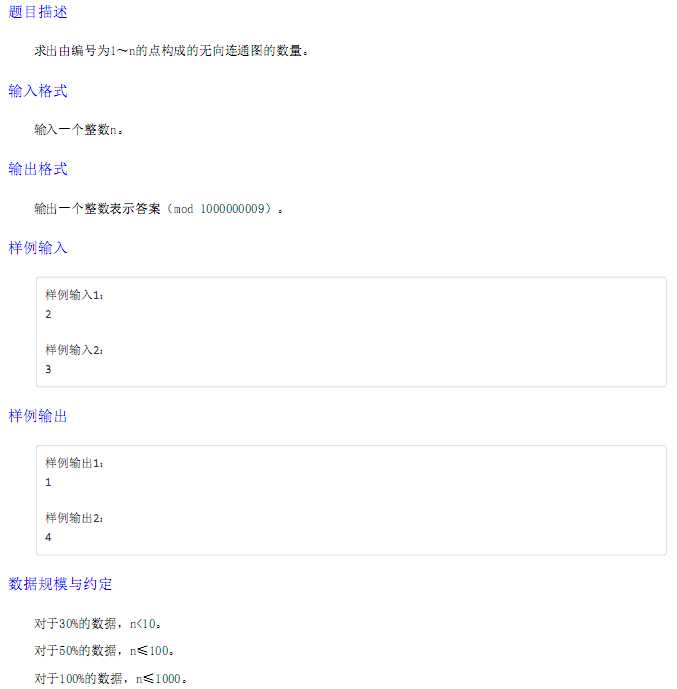
考试时沙雕刚这道题。。。结果学长刚听我解释了一句话就说我凉了。。。的确推了个错式子,对于连通考虑的不清楚qwq
正解:
考虑容斥:对于$n$个点,设所有可能的图有$2^{(n-1)*n/2}$种,记为$h[n]=2^{(n-1)*n/2}$,就是相当于每个边选与不选;
记$f[n]$为$n$个点,连通图的个数,则有:
$f[n]=h[n]-\Sigma_{i=1}^{n-1}C(n-1,i)*f[i]*h[n-i]$
含义:枚举的是与$1$号(或是其他某个节点)相连的点数,$C(n-1,i)$是指从剩下的$n-1$个节点中任取$i$个,然后$f[i]$是与1相连的连通的图的数量,剩下的$n-i$个点随意排列有$h[i]$种;
#include<cstdio> #include<iostream> #define R register int const int M=1010,mod=1000000009; using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } inline int qpow(int a,int b) { register long long ret=1; a%=mod; for(;b;b>>=1,a=(long long)a*a%mod) if(b&1) ret=ret*a%mod; return ret; } int n,f[M],h[M],C[M][M]; signed main() { freopen("graphs.in","r",stdin); freopen("graphs.out","w",stdout); n=g(); for(R i=0;i<=n;++i) { C[i][0]=1; for(R j=1;j<=i;++j) C[i][j]=(long long)(C[i-1][j-1]+C[i-1][j])%mod;//,cout<<i<<" "<<j<<endl;//<<" "<<C[i][j]<<endl; } for(R i=1;i<=n;++i) h[i]=qpow(2,(i-1)*i/2); for(R i=1;i<=n;++i) { f[i]=h[i]; for(R j=1;j<i;++j) f[i]=(f[i]-(long long)C[i-1][j-1]*f[j]%mod*h[i-j]%mod+mod)%mod; f[i]=(f[i]+mod)%mod; } printf("%lld\n",f[n]); }



咕咕咕。。。不是太懂。。。勉强吧、、
#include<cstdio> #include<iostream> #include<cmath> #define db double #define R register using namespace std; int n,m,a,t; db p,mn=1,mx,now,ans; signed main() { freopen("pencil.in","r",stdin); freopen("pencil.out","w",stdout); scanf("%d%d%d%d",&t,&n,&m,&a); while(t--) { scanf("%lf",&p); mn=min(mn,p),mx=max(mx,p); now=pow(p,n); ans=0; for(R int i=n;i>=m;--i) ans+=now,now=now*i*(1-p)/(n-i+1)/p; //printf("%.4lf",ans); R int tmp = ans * 10000 + 0.5; printf("%d.%04d", tmp / 10000, tmp % 10000); putchar(‘\n‘); } printf("%.2lf",n*a*(mx+mn)/2); }
Alice 发现了一处远古宝藏,她想召集一个寻宝队伍帮她去探险。
可供选择的队员一共有 n 个,能力值分别是 {1,2,3,?,n}。Alice 的队伍要求有 m 个队员,其中 m 为奇数。
对于一个队伍,我们记录这个队伍队员能力值的中位数为这个队伍的能力值。
由于 Alice 实在没空一个一个挑选队员,于是她从 n 个选择对象里随机选出 m 个组成队伍。她想知道这样所组成的队伍的能力值的期望是多少。
为了方便答案的比较,设 E 为队伍能力值的期望,你只需要 意义下的值即可。
输入共一行两个正整数 n,m。
输出题是要求的答案在模 p 意义下的值。
3 1
6
对于前 30%的数据,m≤n≤10^6;
对于额外 30%的数据,m≤10^3,n≤10^9;
对于 100%的数据,m≤10^6,n≤10^9,m≤n。
咕咕咕。。。
2019.05.20
原文:https://www.cnblogs.com/Jackpei/p/10888382.html