数据结构丨链表

今天开始学习LeetCode explore上的数据结构：https://leetcode-cn.com/explore/，不定时更新。

单链表

简介

单链表中的每个结点不仅包含值，还包含链接到下一个结点的引用字段。通过这种方式，单链表将所有结点按顺序组织起来。

下面是一个单链表的例子：

蓝色箭头显示单个链接列表中的结点是如何组合在一起的。

结点结构

以下是单链表中结点的典型定义：

struct SinglyListNode {
    int val;
    SinglyListNode *next;
    SinglyListNode(int x) : val(x), next(NULL) {}
};

操作

与数组不同，我们无法在常量时间内访问单链表中的随机元素。 如果我们想要获得第 i 个元素，我们必须从头结点逐个遍历。 我们按索引来访问元素平均要花费 O(N)时间，其中 N 是链表的长度。

例如，在上面的示例中，头结点是 23。访问第 3 个结点的唯一方法是使用头结点中的“next”字段到达第 2 个结点（结点 6）; 然后使用结点 6 的“next”字段，我们能够访问第 3 个结点。

你可能想知道为什么链表很有用，尽管它在通过索引访问数据时（与数组相比）具有如此糟糕的性能。 在接下来的两篇文章中，我们将介绍插入和删除操作，你将了解到链表的好处。

之后，我们将为你提供练习设计自己的单链表。

添加操作

如果我们想在给定的结点 prev 之后添加新值，我们应该：

1. 使用给定值初始化新结点 cur；
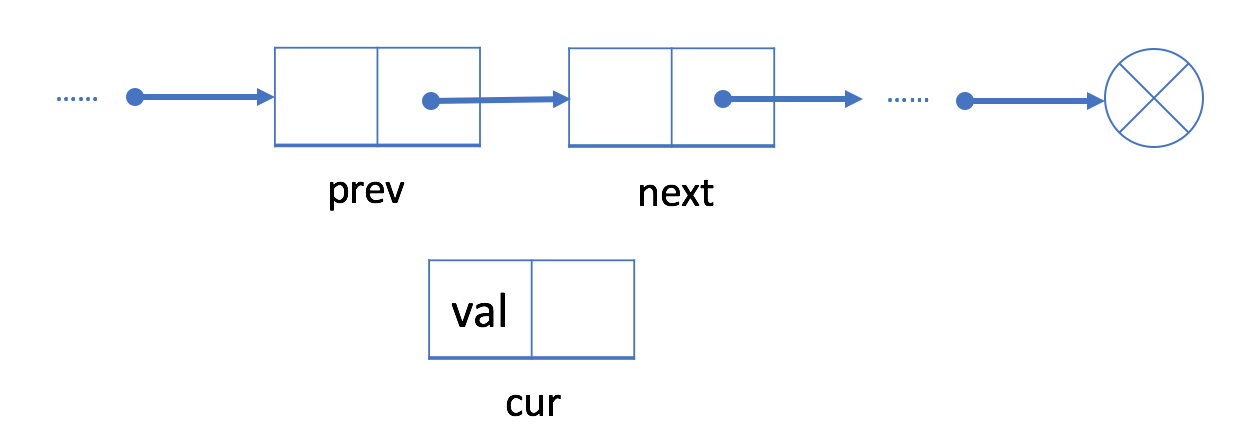
2. 将 cur的“next”字段链接到 prev 的下一个结点 next；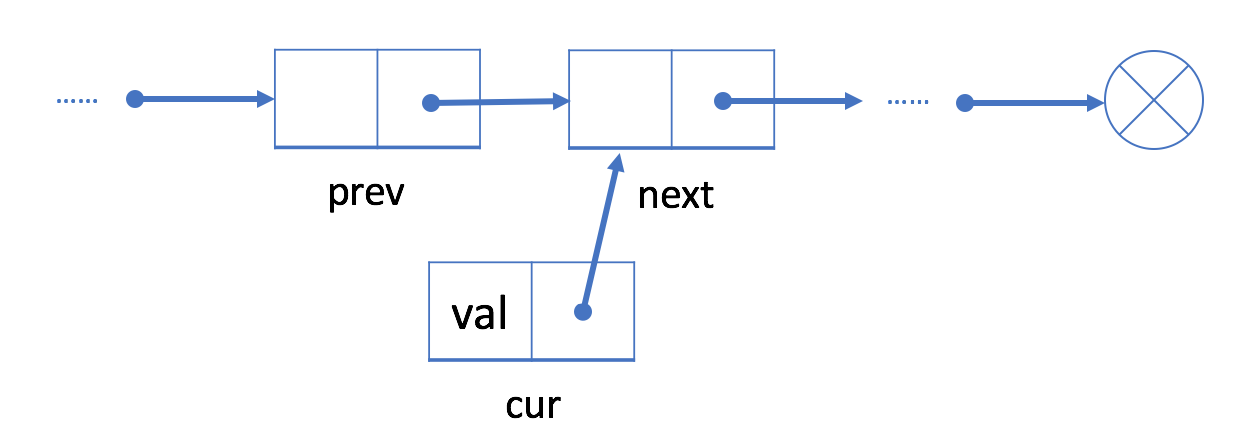
3. 将 prev 中的“next”字段链接到 cur 。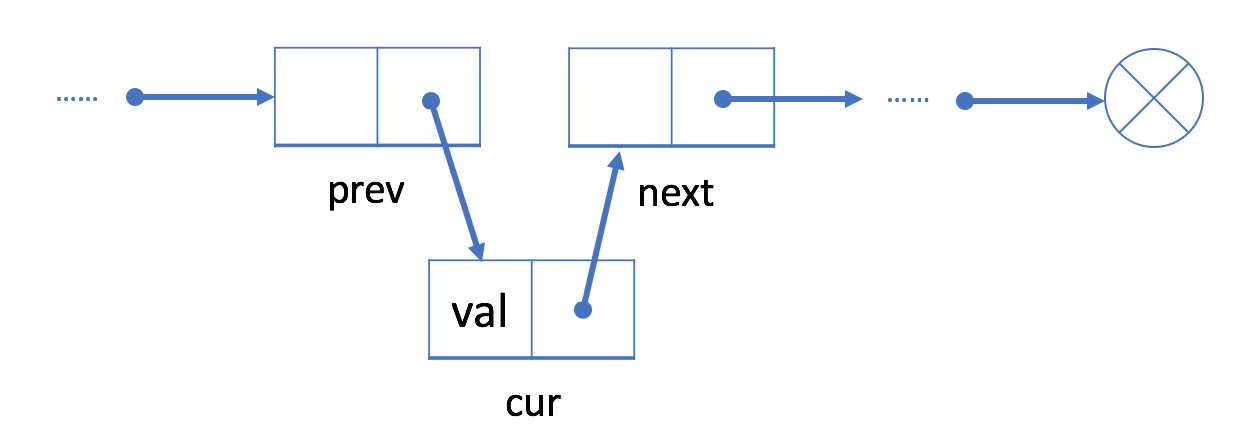

与数组不同，我们不需要将所有元素移动到插入元素之后。因此，您可以在 O(1) 时间复杂度中将新结点插入到链表中，这非常高效。

示例

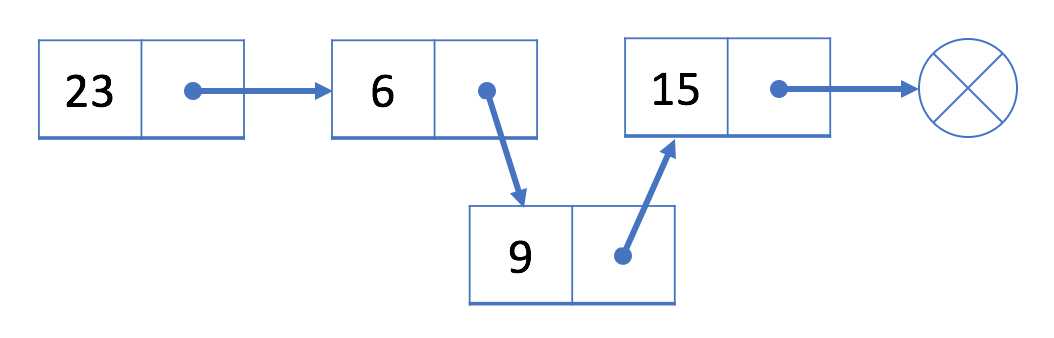
让我们在第二个结点 6 之后插入一个新的值 9。

我们将首先初始化一个值为 9 的新结点。然后将结点 9 链接到结点 15。最后，将结点 6 链接到结点 9。

插入之后，我们的链表将如下所示：

在开头添加结点

众所周知，我们使用头结点来代表整个列表。

因此，在列表开头添加新节点时更新头结点 head 至关重要。

1. 初始化一个新结点 cur；
2. 将新结点链接到我们的原始头结点 head。
3. 将 cur 指定为 head。

例如，让我们在列表的开头添加一个新结点 9。

1. 我们初始化一个新结点 9 并将其链接到当前头结点 23。
2. 指定结点 9 为新的头结点。

如何在列表的末尾添加新的结点？我们还能使用类似的策略吗？

删除操作

如果我们想从单链表中删除现有结点 cur，可以分两步完成：

1. 找到 cur 的上一个结点 prev 及其下一个结点 next；
2. 接下来链接 prev 到 cur 的下一个节点 next。

在我们的第一步中，我们需要找出 prev 和 next。使用 cur 的参考字段很容易找出 next，但是，我们必须从头结点遍历链表，以找出 prev，它的平均时间是 O(N)，其中 N 是链表的长度。因此，删除结点的时间复杂度将是 O(N)。

空间复杂度为 O(1)，因为我们只需要常量空间来存储指针。

示例

让我们尝试把结点 6从上面的单链表中删除。

1. 从头遍历链表，直到我们找到前一个结点 prev，即结点 23

2. 将 prev（结点 23）与 next（结点 15）链接

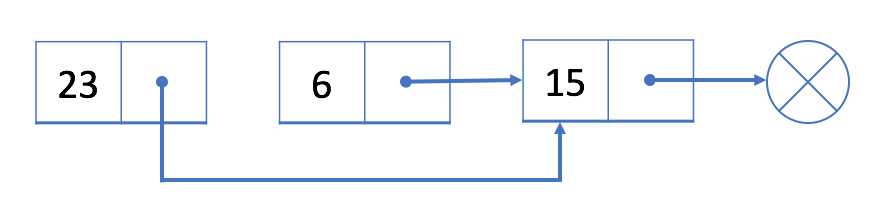
结点 6 现在不在我们的单链表中。

删除第一个结点

如果我们想删除第一个结点，策略会有所不同。

正如之前所提到的，我们使用头结点 head 来表示链表。我们的头是下面示例中的黑色结点 23。

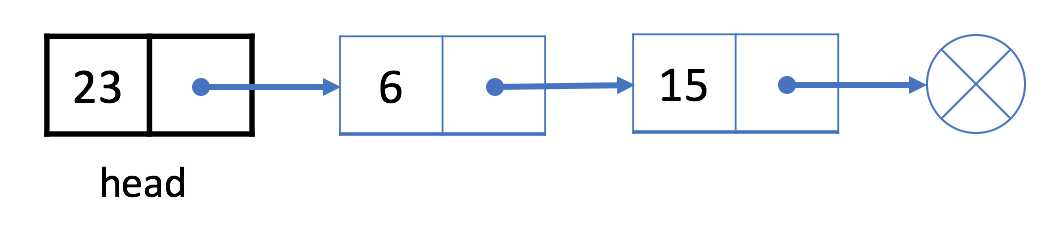
如果想要删除第一个结点，我们可以简单地将下一个结点分配给 head。也就是说，删除之后我们的头将会是结点 6。

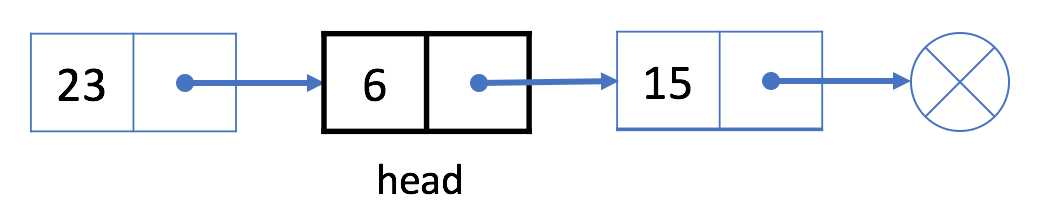
链表从头结点开始，因此结点 23 不再在我们的链表中。

删除最后一个结点呢？我们还能使用类似的策略吗？

设计链表

设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。

在链表类中实现这些功能：

• get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
• addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
• addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
• addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。
• deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

示例：

MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2);   //链表变为1-> 2-> 3
linkedList.get(1);            //返回2
linkedList.deleteAtIndex(1);  //现在链表是1-> 3
linkedList.get(1);            //返回3

提示：

• 所有值都在 [1, 1000] 之内。
• 操作次数将在 [1, 1000] 之内。
• 请不要使用内置的 LinkedList 库。

#include <iostream>

using namespace std;

class MyLinkedList
{
private:
    class Node
    {
    public:
        int val;
        Node *next;

        Node(int val, Node *next) : val(val), next(next) {}
        Node(int val) : Node(val, NULL) {}
    };

public:
    Node *head;
    MyLinkedList()
    {
        head = NULL;
    }

    int get(int index)
    {
        Node *cur = head;
        for (int i = 0; i < index && cur; i++)
            cur = cur->next;
        if (!cur || index < 0)
            return -1;
        return cur->val;
    }

    void addAtHead(int val)
    {
        head = new Node(val, head);
    }

    void addAtTail(int val)
    {
        if (head == NULL)
            head = new Node(val);
        else
        {
            Node *cur = head;
            while (cur->next)
                cur = cur->next;
            cur->next = new Node(val);
        }
    }

    void addAtIndex(int index, int val)
    {
        if (index <= 0)
            addAtHead(val);
        else
        {
            Node *cur = head;
            for (int i = 1; i < index && cur; i++)
                cur = cur->next;
            if (cur)
                cur->next = new Node(val, cur->next);
        }
    }

    void deleteAtIndex(int index)
    {
        if (index == 0)
        {
            if (head)
            {
                Node *delNode = head;
                head = head->next;
                delete delNode;
            }
        }
        else
        {
            Node *cur = head;
            for (int i = 1; i < index && cur; i++)
                cur = cur->next;
            if (cur && cur->next && index > 0)
            {
                Node *delNode = cur->next;
                cur->next = delNode->next;
                delete delNode;
            }
        }
    }
};

// int main()
// {
//     MyLinkedList list = MyLinkedList();
//     list.addAtHead(1);
//     list.addAtTail(3);
//     list.addAtIndex(1, 2);
//     list.get(-1);
//     list.deleteAtIndex(1);
//     list.get(-3);
// }

链表中的双指针

经典问题

双链表

小结

数据结构丨链表

原文：https://www.cnblogs.com/vincent1997/p/10897325.html