OO第三单元总结——JML规格设计

• (1)梳理JML语言的理论基础、应用工具链情况

• (2)【改为选做，能较为完善地完成的将酌情加分】部署SMT Solver，至少选择3个主要方法来尝试进行验证，报告结果

    • 有可能要补充JML规格

• (3)部署JMLUnitNG/JMLUnit，针对Graph接口的实现自动生成测试用例（简单方法即可，如果依然存在困难的话尽力而为即可，具体见更新通告帖）， 并结合规格对生成的测试用例和数据进行简要分析

• (4)按照作业梳理自己的架构设计，并特别分析迭代中对架构的重构

作业一、MyPathContainer规格设计

1. 统计信息图

2. 复杂度分析

基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

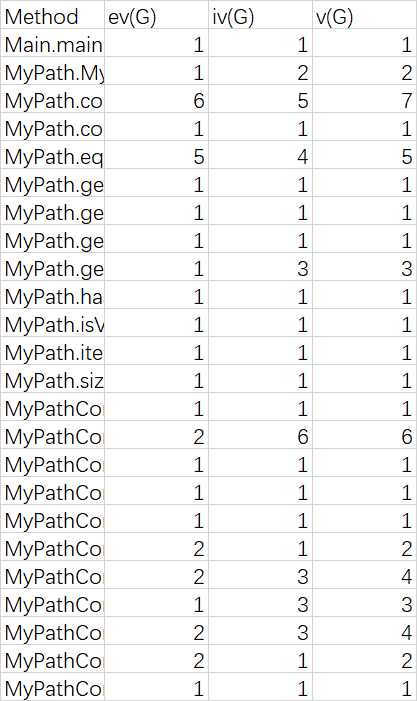
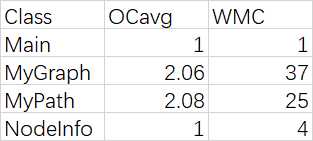
OCavg为平均循环复杂度;WMC为总循环复杂度

3. 结构信息图

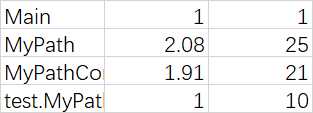
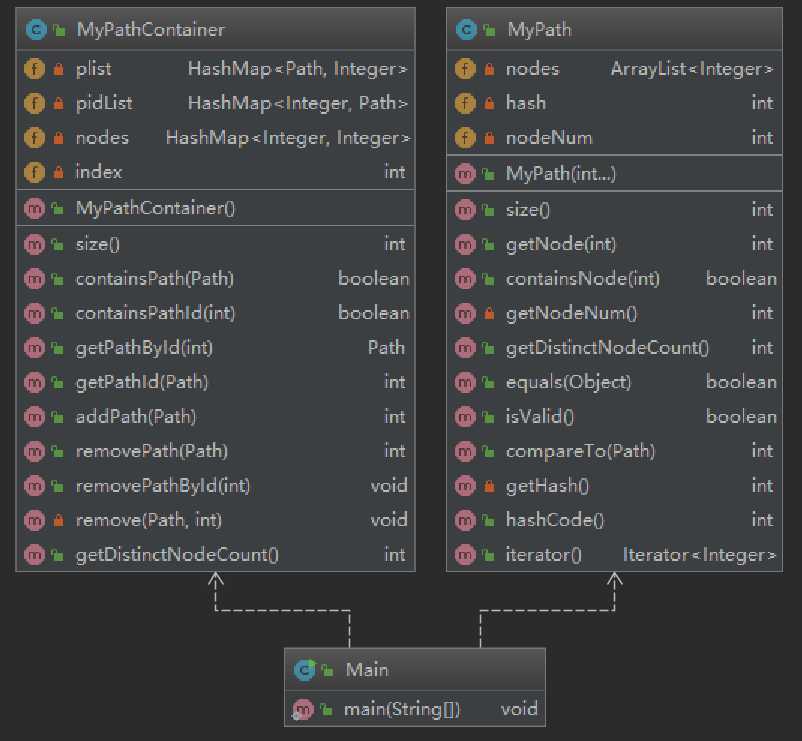
可见，由于逻辑简单，本次作业的复杂度和耦合度都不高。 

4. 分析架构设计

为了减少时间复杂度，采用的是三个hashmap的策略，效果良好。也为以后减少时间开销打下了基础。

作业二、MyGraph规格设计

1. 统计信息图

2. 复杂度分析

基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

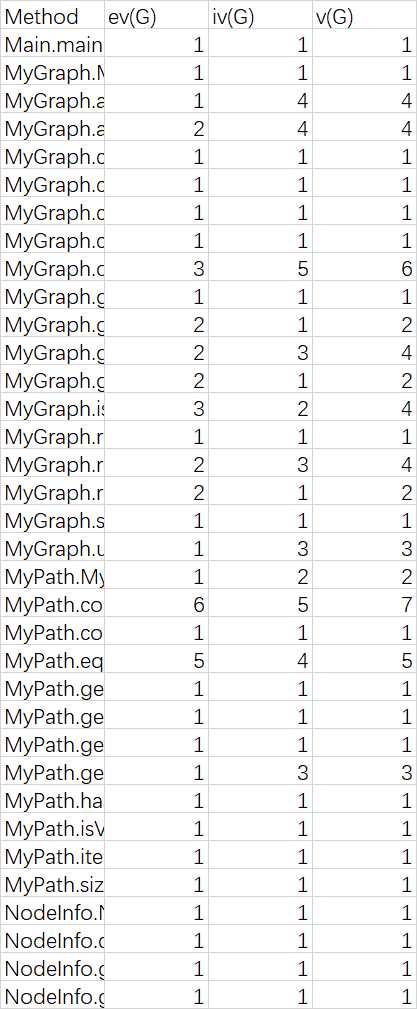
OCavg为平均循环复杂度;WMC为总循环复杂度

3. 结构信息图

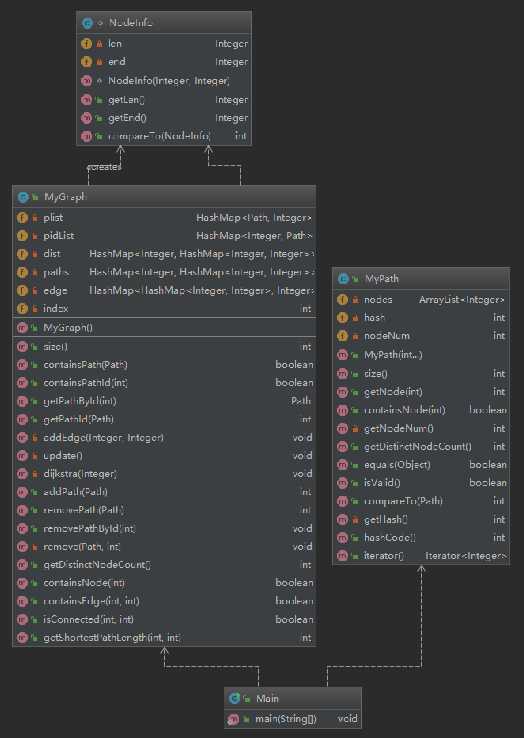
可见，由于逻辑简单，本次作业的复杂度和耦合度都不高。 

4. 分析架构设计

在上一次作业的基础上，采用使用优先队列的迪杰斯特拉算法实现最小路径，并将中间结果储存，减少重复计算，以最大化减少运行时间。

但是架构设计不好，上一次作业的内容直接复制粘贴，应该采用集成的方式实现。对下一次作业也不友好，没有对迪杰斯特拉算法建模或单独建类。

作业三、MyRailwaySystem规格设计

1. 统计信息图

2. 复杂度分析

基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度

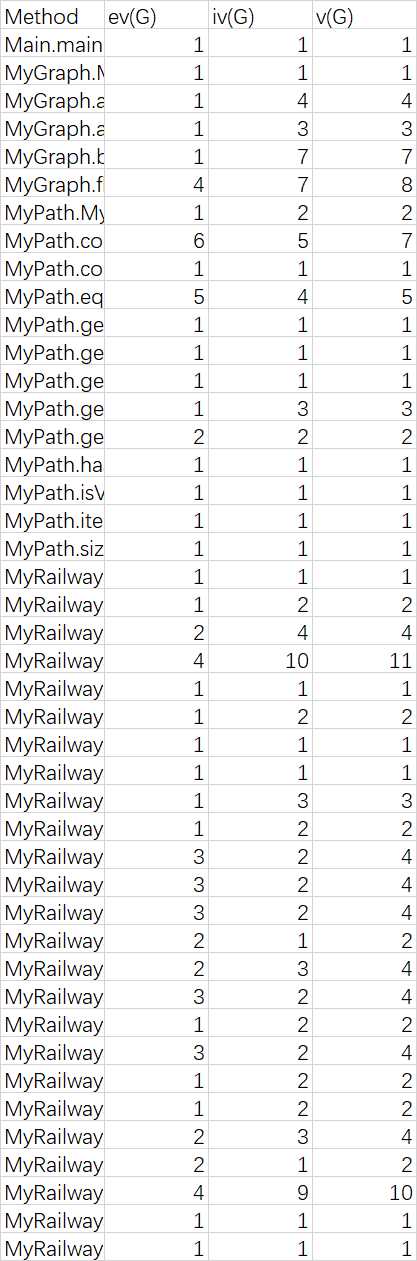
OCavg为平均循环复杂度;WMC为总循环复杂度

3. 结构信息图

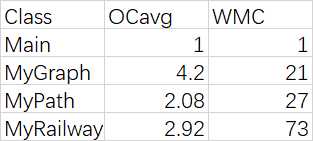
可见，由于逻辑简单，本次作业的复杂度和耦合度都不高。  

4. 分析架构设计

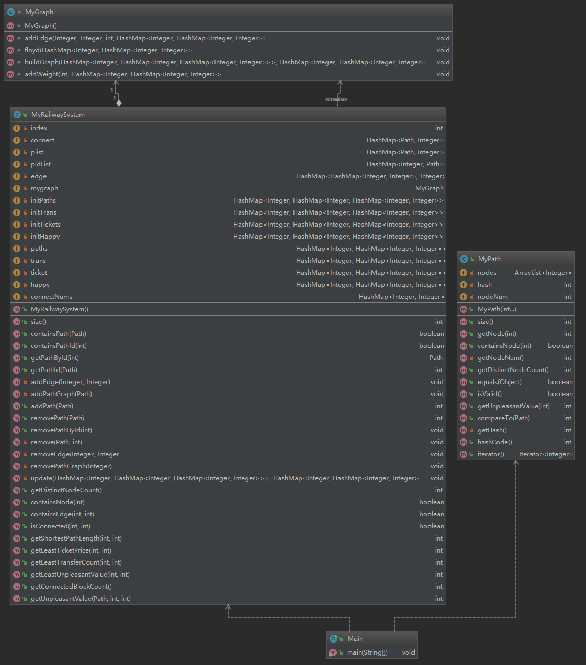
　　在上次作业的基础上，进行了一定的重构，首先是将迪杰斯特拉和弗洛伊德等最短路径算法分离出去，单独建类，并将对于图的有关操作单独建类。其次，模型采用评论区大佬的“完全图方法”，主要算法是弗洛伊德算法，保存所有中间矩阵和初始建图矩阵。

• (5)按照作业分析代码实现的bug和修复情况

第一次作业中未出现BUG

第二次作业中未出现BUG

第三次作业中出现一个BUG，出错点是判断连通块个数出错。

　　我判断连通块是通过遍历paths中所有的path，如含有path_new中的点，则将两者判为连通块。

　　出错原因：当pathA和pathB连通时，pathC加入，若pathA中含有pathC中点，pathB中不含有pathC中的点，那么我会判断pathA和pathC连通，但是判断pathB和pathC不连通，与实际不符。

　　解决措施：在判断时，将所有与path_new连通的path的标志号记下，最后再遍历一遍paths，将所有标志号在其中的path，判断与path_new连通。

• (6)阐述对规格撰写和理解上的心得体会

OO第三单元总结——JML规格设计

原文：https://www.cnblogs.com/Guo-mengqi/p/10899615.html