求解最优化问题中,拉格朗日乘子法和KKT条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法,在有不等式约束时使用KKT条件。这个最优化问题通常指某一函数在指定作用域上的全局最小值(最小值与最大值可以相互转换)。
最优化问题通常有三种情况(这里说两种):
1. 无约束条件
求解办法是令导数等于0得到极值点。将结果带回原函数验证。
2. 等式约束条件
设目标函数f(x),约束条件hk(x),
min f(x) s.t. hk(x)=0 (k = 1,2...l)
l表示有l个约束条件。
该类问题解决办法是消元法或拉格朗日法。消元法简单,这里讲拉格朗日法,后面提到的KKT条件是对拉格朗日乘子法的泛化。
例子:
椭球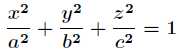 内接长方体的最大体积,即求 f(x,y,z) = 8xyz 的最大值。
内接长方体的最大体积,即求 f(x,y,z) = 8xyz 的最大值。
方法1:消元法
根据条件消去z,然后带入函数转化为无条件极值问题。(有时这种方法麻烦,甚至解不出来)
方法2:拉格朗日乘法
首先定义拉格朗日函数F(x):
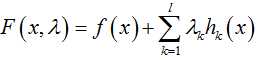 (λk是各个约束条件的待定系数)
(λk是各个约束条件的待定系数)
对各个变量求偏导:
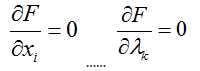
如果有 l 个约束条件,就应该有 l+1 个方程。方程组的解就可能是最优化值,将结果带回原方程验证。
上面的函数,通过拉格朗日乘数法将问题转化为:
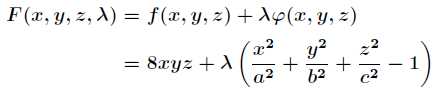
对 F(x,y,z,λ) 求偏导得到
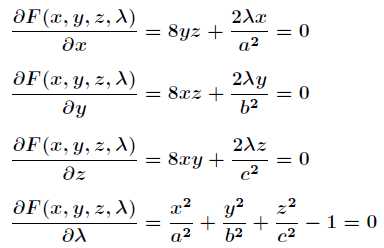
联立前面3个方程得到 bx = ay 和 az = cx,带入第4个方程:
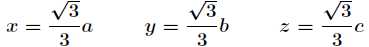
带入原函数得到最大体积:
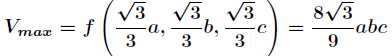
为什么这么做是最优解?
举个例子:min f(x,y) s.t. g(x,y) = c
画出 z = f(x,y)的等高线
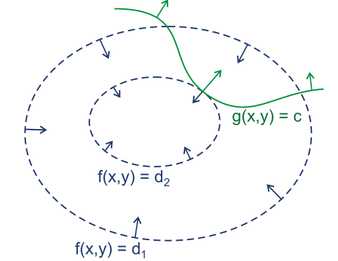
绿线是约束g(x,y) = c的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率,和等高线的发现平行。从梯度的方向看,d1>d2。
在没有约束条件,f(x,y)的最小值是落在最里面等高线内部的某一点。加上约束条件的 f(x,y) 最小值是 f(x,y)的等高线和约束线相切的位置,因为如果只是相交意味着还存在其它的等高线在该等高线的内部或外部,使新的等高线与目标函数的交点值更大或更小,只有等高线与目标函数的曲线相切时,取到最优值。
原文:https://www.cnblogs.com/keye/p/10916118.html