决策树
决策树是一种强大的算法,可解释性强,对复杂数据集的拟合能力强,对数据集的前期处理(如特征缩放,集中等)要求很少。它的工作原理是,在每个节点上选取一个特征作为分类依据,并给定阈值,根据阈值来将实例归为左子树或右子数,然后对子节点进行同样的特征选取和阈值给定,直至所有节点上的实例都属于同一类别或者没有特征可用,此时的节点就是叶节点。实际应用中一般会设定一个决策树的深度,以免造成过拟合。决策树可以做分类或回归。
在sklearn的DecisionTreeClassifier工具中,每个节点包含特征及阈值,sample(训练实例数),gini(基尼不纯度),类别。基尼不纯度定义为:
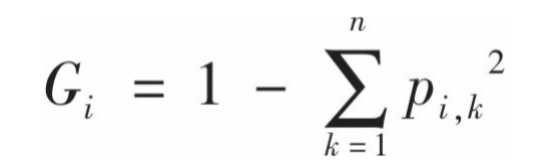
表征的是每个节点上混入的不同类别的程度。i为节点标号,n为节点上实例个数,Pi,k为类别为k的比例。
决策树还可以估算实例属于某个类别(k)的概率,这是因为每个节点上的实例数都是可以计算的。首先找到该实例的叶节点,然后返回该节点中类别k的实例占比。在sklearn中实例类别和概率都可以返回,只需要调用相应的函数:
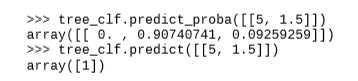
sklearn默认使用的是CART(classification and regression tree,分类与回归树),该算法只生成二叉树。其想法简单,首先使用单个特征k和阈值tk将训练集分为两个子集。k和tk如何选择呢?答案是k和tk应当产生最纯子集。该算法尝试最小化以下成本函数:

一旦将成功将训练集一分为二,然后使用相同的逻辑对子集进行划分,然后是子集的子集,直到最大深度,或是不纯度无法再降低。它是一个贪婪算法,因为它只会计算当前情况下的最优情况,而不会检视这个决策在全局层面是否是全局最优。然而,寻找最优树是一个很棘手的问题,其计算复杂度很高,因此我们往往接受一个“相当不错的近似解”。
它的不足之处在于它的计算复杂度。一般地,生成的树比较平衡,预测时,从 根节点开始,每个节点只需要比较一个特征值,其计算复杂度为![]() ,与特征数量无关,因此即使是处理大数据集,预测也很快。然而在训练时,在每一个节点,算法都要在所有样本上比较所有特征,其计算复杂度为
,与特征数量无关,因此即使是处理大数据集,预测也很快。然而在训练时,在每一个节点,算法都要在所有样本上比较所有特征,其计算复杂度为![]() ,当数据集较大是,速度可能变慢。
,当数据集较大是,速度可能变慢。
决策树很少对数据做出假设(例如数据线性可分),因此具有高自由度,对数据拟合能力强,这是它的优势,但也可能成为缺点,因为如果不加以控制,就容易在训练集上导致过拟合。限制自由度可以降低过拟合的风险,但增加了拟合不足的风险。正则化的实质就是限制自由度。在skleran的决策树工具包中有很多可供选择的参数来限制自由度。还可以通过剪枝对不必要的节点删除:不加约束的训练模型,然后根据某种规则对节点进行简化(比如某个节点的子节点都是叶子节点,则该节点可以被删除)。
决策树回归
决策树也可以用于回归,这时模型输出的就是一个预测值。skleran中决策树用于回归采用的还是CART算法,这时分裂数据集的方法是最小化MSE,成本函数如下:
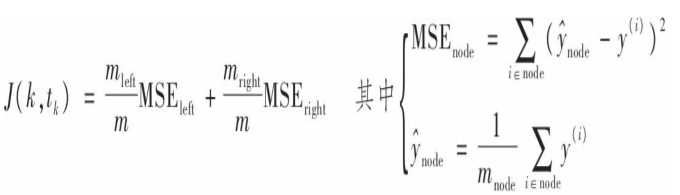
从上式可知,每个根节点的值就是该节点下所有实例的均值,算法通过调整每个子树上的实例数来最小化MSE。预测输出值就是与输入实例在同一叶子节点上的所有实例的均值。
不稳定性
决策树的不稳定体现在它对数据的微小变化很敏感,这些变化包括数据集的旋转,某些类别的实例的增减等。对于旋转问题要使用PCA方法来使数据定位在一个更好的方向上。更重要的是我们可以用随机森林来限制决策树的不稳定性。
集成学习和随机森林
这是群体智慧的体现。通过训练一组决策树分类器,每棵树都使用训练集不同的随机子集来训练,然后获得每棵树对输入实例的预测,将得票最多的类别作为预测结果。这种集成方法并不要求所要训练的一组模型完全是相同的,只需要保证它们能够输出相同信息,比如都能够输出概率值,然后根据所有的概率值做平均。这种集成方法往往比单个分类器得到的结果要好得多,只要有足够的数据和模型可用。最好是使用一组互不相同的弱分类器。因为集成方法在弱分类器彼此独立时效果最好,但是每种弱分类器都会犯错,使用多个同样的弱分类器,意味着它们很可能会犯同样的错误。为何弱分类器的简单组合就能得到如此好的结果呢?这背后是大数定理在起作用。如果所有单个分类器都能给出概率,那么将平均概率最高的类别作为预测类别,这就是软投票法,它通常比硬投票法好一点,因为它给予那些高度自信的投票(就是概率值大)更高的权重(硬投票大将所有投票的权重同等对待)。
bagging 和 pasting
如果所有算法模型都相同,但是在不同的训练集随机子集上进行训练,如果采样时将样本放回就叫bagging,如果不放回就叫pasting。
用于分类时,通过软或硬投票聚合法完成,用于回归时通过平均法完成。
集成后的结果一般偏差相近,但方差更小。
你可以并行地训练多个模型,这也是bagging和pasting如此流行的重要原因。
Random patches 和 随机子空间
sklearn 的BaggingClassifier也支持对特征的抽样,这种抽样为预测期带来了更大的多样性,因此往往导致更大的偏差和更小的方差。如果对实例和特征同时进行随机抽样,这被称为random patches,如果保留所有训练实例而只对特征抽样就称为随机子空间。
随机森林
随机森林在树的生长上引入了更多的随机性:分裂节点时不再是搜索最好的特征而是在一个随机特征子集里搜寻最好的特征,这种多样性同样带来更大的偏差和更小的反差。
极端随机树
它在一般随机森林的基础上,对每个特征使用随机阈值,而不是搜寻最好的阈值,这带来更大的随机性,当然其后果也是相同的。它训练起来比随机森林快得多,因为在每个节点上找每个特征值的最佳阈值是决策树生长中最耗时的任务。一般地,randomForest和极端树哪一个更好事先是不确定的,最好是使用交叉验证,选择最合适的。
特征重要性
决策树还为我们提供了评估特征重要性的方法。你可以发现最重要的特征往往出现在树的根节点,而不重要的特征更靠近叶子节点,甚至根本不出现。因此通过计算特征在森林的所有树中的平均深度,可以估算出一个特征的重要程度。所有,如果你需要了解特征的重要程度,随机实例可以提供十分便利的帮助!
提升法
前面提到的集成方法中,每个预测器的结果互不影响,而在提升法中,多个弱分类器的训练是窜行进行的,前一个预测期的输出结果会引导后一个预测期作出更合理的预测。通过分析前一个分类器所作出的错误的预测,对这些预测错误的实例赋予更高的权重,将调整后的权重作为下一个预测器的输入权重,这样就能使下一个预测器更专注于难缠的问题。最后所有预测器完成训练后,其集成方法和一般集成方法是一样的(软或硬投票)。这就叫做AdaBoost。因为它不能并行,因此扩展性不好。
仔细看一下Adaboost算法的原理:在开始时每个实例的权重设置为w(i)=1/m,m为实例总数。第一个预测器训练后,其加权误差率为:

预测器的权重alpha(j)由下式求得:
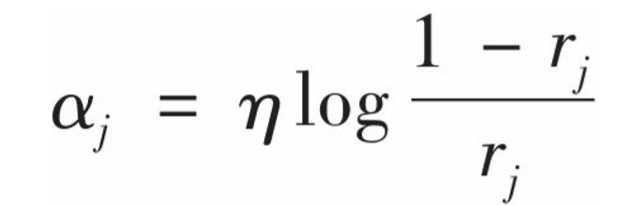
theta是控制学习率的超参数。通过上式,对准确率较高的预测器更高的权重。如果一个预测器近乎随机,那么r(j)接近0.5,于是alpha(j)接近于0,如果预测器大多数时候都是错误的吗,那么它的权重为负。
权重更新:
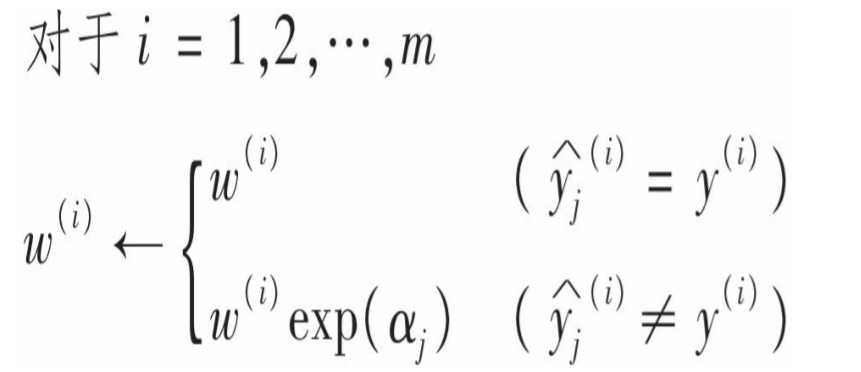
这里有两层意思:1.已经预测准确的实例权重不变,只关注预测错误的实例,增加其权重;2. 预测器准确率越高的权重增加越多。
这里还需要将权重归一化。权重更新后,重新训练一个新的预测器,重复以上过程,直至满足预测器的数目,或者模型已经足够好。预测时,Adaboost对所有预测器的结果根据预测器的权重进行加权,得到大多数加权投票的类别就是预测的类别。所以这里alpha有两个作用,一是在训练过程中直接影响预测错误的实例的权重;而是在最终做出预测时,直接影响每个预测器输出结果的权重。
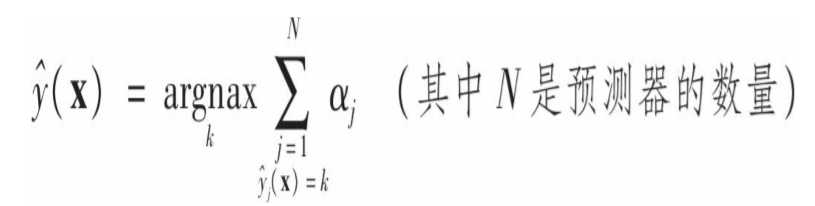
梯度提升法
这也是一种窜行集成的方法,每一个预测器都对前序做出修正,不同的是它不是调整权重,而是让新的预测器对前一个预测器的残差进行拟合。最后做出预测时是将所有预测器的输出进行求和(作为回归时)。那么如何选择树的最佳数目呢?有两种方法:
1. 使用两个GRBT(grident regression boosting tree),在训练过程中使用一个GRBT,每次迭代时都会计算验证误差,结束后找出最优的树的数量,然后重新训练一个GRBT;
2. 通过设置一些参数来进行增量训练,当验证误差在给定迭代次数中变化很小时可以停止训练,这是一种真正的早期停止法。
堆叠法
堆叠法的诀窍在于将原始训练集分为两个子集,并在此基础上生成第三个子集。与之相对应,它也有三层训练。在一个子集上训练预测器,然后在另一个“新鲜的”的子集上进行预测,输出的预测值作为第三层预测器的输入特征(这时特征的维度变为n维,n是预测器的个数),最后通过聚合产生新的预测结果。当新实例来时,通过顺序进行以上三层预测器得到最终的预测结果。注意,第三层预测器训练时的目标值是第一层的目标值。
原文:https://www.cnblogs.com/gadflyWZQ/p/10891461.html