拉格朗日插值法是一个根据点对求回原函数的算法,原理挺好懂的。
推荐博客:https://www.cnblogs.com/zwfymqz/p/10063039.html#_label1_0
原理是优化方法上面的大佬都讲得很好。
其实主要就是这个式子: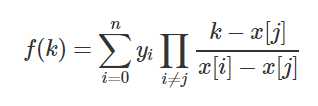
然后暴力算这个式子的话是每求一项f(k)的时间复杂度都是n^2。
这个时间很不优秀,于是我们想办法在一些特殊时候优化它。
在x连续的时候我们可以通过预处理的方式加快速度,式子为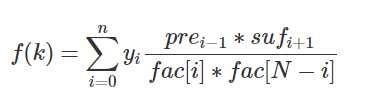
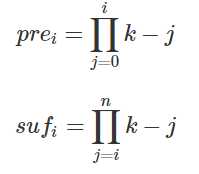
然后其实拉格朗日插值就上面两个式子,具体题目的具体点对不一样,但是插值的方法就是这样。

然后重心拉格朗日插值法就是把朴素的式子变形,它的好处是
虽然原理好懂代码好写,但是做题并不好做,得看出所求函数是几次多项式也得简略证明一下,这要求有一定的数学素养。这一个知识点蒟蒻还是差得很多,基本上就是做一题看一题题解。主要是虽然拉格朗日插值法不难,也好些。但是架不住我根本不知道要求的是哪个函数呀qwq qwq qwq,这样的话初始点对都求不出来,那还插个球。。。
不管怎样,一定不能有式子恐惧症,要多加训练推式子的能力。加上这个知识点不怎么熟练,一定要回看。
题目练习:
洛谷P4781
模板题:

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=2e3+10; const int MOD=998244353; int n,k,x[N],y[N]; int power(LL x,LL p,LL MOD) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%MOD; x=x*x%MOD; } return (int)ret; } int Lagrange() { int ret=0; for (int i=1;i<=n;i++) { int up=1,down=1; for (int j=1;j<=n;j++) { if (i==j) continue; up=(LL)up*((k-x[j])%MOD+MOD)%MOD; //分子 down=(LL)down*((x[i]-x[j])%MOD+MOD)%MOD; //分母 } int tmp=(LL)y[i]*up%MOD*power(down,MOD-2,MOD)%MOD; ret=(ret+tmp)%MOD; } return ret; } int main() { cin>>n>>k; for (int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]); cout<<Lagrange()<<endl; return 0; }
洛谷P4593
看大佬题解,主要矛盾就是算sigma(i^m) (i=1~m+1) 这个用拉格朗日插值法可以解决。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=100; const int P=1e9+7; int n,m; LL jc[N],pre[N],suf[N],a[N],y[N]; void prework() { jc[0]=1; for (int i=1;i<=60;i++) jc[i]=(jc[i-1]*i)%P; } LL power(LL x,LL p,LL MOD) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%MOD; x=x*x%MOD; } return ret; } //拉格朗日插值计算:sigma(i^m) (i=1~m+1) 因为计算m项要用m+1个点 LL Lagrange(int n) { LL ret=0; pre[0]=n; for (int i=1;i<=m+1;i++) pre[i]=(pre[i-1]*(n-i))%P; //预处理分子前缀 suf[m+2]=1; for (int i=m+1;i;i--) suf[i]=(suf[i+1]*(n-i))%P; //预处理分母后缀 for (int i=1;i<=m+1;i++) { //m+1个点插点 LL up=pre[i-1]*suf[i+1]%P; LL down=jc[i]*jc[m+1-i]%P; if ((m+1-i)%2==1) down=P-down; //注意,(m+1-i)奇数项分母取反 LL tmp=up*power(down,P-2,P)%P*y[i]%P; ret=(ret+tmp)%P; } return ret; } int main() { prework(); int T; cin>>T; while (T--) { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) scanf("%d",&a[i]); a[++m]=++n; sort(a+1,a+m+1); for (int i=1;i<=m+2;i++) y[i]=power(i,m,P); for (int i=1;i<=m+2;i++) y[i]=(y[i]+y[i-1])%P; //算出(x,y)点对 LL ans=0; for (int i=1;i<=m;i++) { //计算ans for (int j=i;j<=m;j++) ans=(ans+Lagrange(a[j]-1)-Lagrange(a[j-1]))%P,ans=(ans+P)%P; for (int j=i+1;j<=m;j++) a[j]=a[j]-a[i]; a[i]=0; } printf("%lld\n",ans); } return 0; }
BZOJ-3453
惭愧的说,这题我现在还是不能完全理解为什么就能表示成K+4次多项式。但是其实能看出来的话也是直接插值就可以了。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const LL P=1234567891; const LL N=200+10; LL k,a,n,d; LL f[N],g[N]; LL power(LL x,LL p,LL MOD) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%MOD; x=x*x%MOD; } return ret; } //计算k项式(i,f[i])的第n项 LL Lagrange(LL *f,LL k,LL n) { LL ret=0; for (int i=0;i<=k;i++) { LL up=f[i],down=1; for (int j=0;j<=k;j++) { if (i==j) continue; up=up*((n-j+P)%P)%P; down=down*((i-j+P)%P)%P; } ret=(ret+up*power(down,P-2,P)%P)%P; } return ret; } int main() { int T; cin>>T; while (T--) { memset(f,0,sizeof(f)); memset(g,0,sizeof(g)); scanf("%lld%lld%lld%lld",&k,&a,&n,&d); for (int i=1;i<=k+4;i++) f[i]=power(i,k,P); for (int i=1;i<=k+4;i++) f[i]=(f[i-1]+f[i])%P; for (int i=1;i<=k+4;i++) f[i]=(f[i-1]+f[i])%P; for (int i=0;i<=k+4;i++) g[i]=((i>0?g[i-1]:0)+Lagrange(f,k+4,a+i*d))%P; printf("%lld\n",Lagrange(g,k+4,n)); } return 0; }
原文:https://www.cnblogs.com/clno1/p/10920454.html