上一节我们学习knn,kNN的最大缺点就是无法给出数据的内在含义,而使用决策树处理分类问题,优势就在于数据形式非常容易理解。
决策树的算法有很多,有CART、ID3和C4.5等,其中ID3和C4.5都是基于信息熵的,也是我们今天的学习内容。
1. 信息熵
熵最初被用在热力学方面的,由热力学第二定律,熵是用来对一个系统可以达到的状态数的一个度量,能达到的状态数越多熵越大。香农1948年的一篇论文《A Mathematical Theory of Communication》提出了信息熵的概念,此后信息论也被作为一门单独的学科。
信息熵是用来衡量一个随机变量出现的期望值,一个变量的信息熵越大,那么他出现的各种情况也就越多。信息熵越小,说明信息量越小。
对于信息的定义,可以这样理解,如果待分类的事务划分在多个分类之中,则符号xi的信息定义为
I(xi) = -log2p(xi) 其中p(xi) 是选择该分类的概率
为了计算熵,我们需要计算所有类别所有可能值包含的信息期望值,通过下面的公式可得:
 ,其中n是分类的数目
,其中n是分类的数目
2. 计算信息熵
这里有个小例子,通过2个特征:有无喉结,有无长胡子,来划分男人和女人
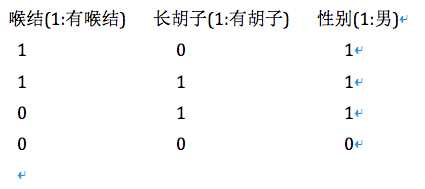
使用python实现简单计算信息熵,程序如下:
from math import log #创建简单数据集 def creatDataset(): dataSet = [[1,1,‘yes‘],[1,1,‘yes‘],[1,0,‘no‘],[0,1,‘no‘],[0,1,‘no‘]] labels = [‘no surfacing‘,‘flippers‘] return dataSet,labels #计算信息熵 def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts = {} for vec in dataSet: currentLabel = vec[-1] if currentLabel not in labelCounts.keys(): #为所有可能的分类建立字典 labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key])/numEntries shannonEnt -= prob * log(prob,2) return shannonEnt #简单测试 myDat,labels = creatDataset() print myDat print calcShannonEnt(myDat)
测试结果如下:
[[1, 1, ‘yes‘], [1, 1, ‘yes‘], [1, 0, ‘no‘], [0, 1, ‘no‘], [0, 1, ‘no‘]] 0.970950594455
得到熵之后,我们就可以按照获取最大信息熵的方法来划分数据集。
原文:http://www.cnblogs.com/chenbjin/p/3906062.html