注意:总结java基础错误
所以想要达到获取修改后的引用的效果,正确的做法应该是:在函数中返回修改后的形参引用,然后在调用代码中,获取这个返回的引用,即可!!(因为想达到,把root根结点传进函数中,创建二叉树。结果一直改变不了root)
栈也是有他独立的空间存储当前的变量值的,如果想要达到递归中 读取一个数组中的数据来创建二叉树,
那么index数组下标索引要设置为全局变量才可以!
所以:凡是涉及到在函数内部,想要修改引用(new (),malloc())的情况,在Java中,必须要返回这个新的引用给原调用函数。
在C语言中,想要修改指针的指向,要用指针的指针
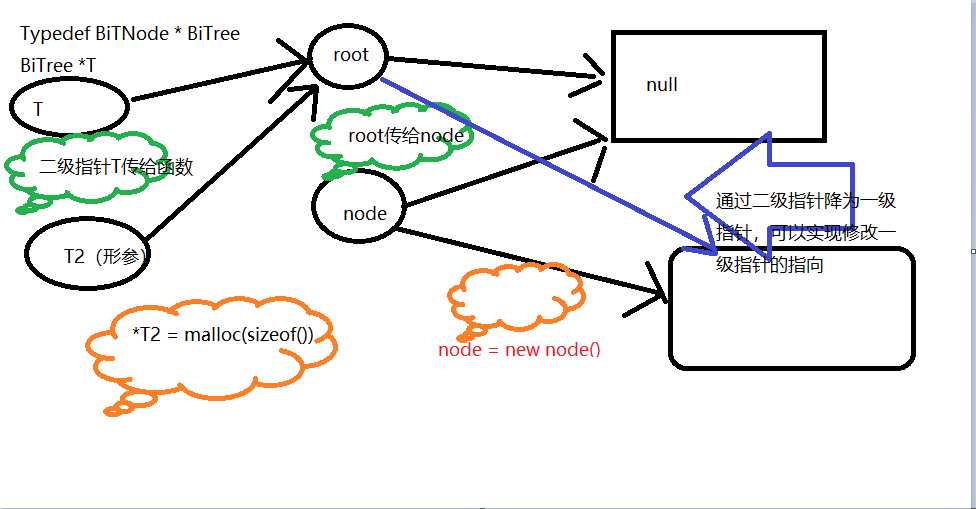
树 完整代码:
/**
* 二叉树
*
*/
public class BinaryTree<T> {
public BinaryTreeNode root;
public static int index = 0;
public BinaryTree(){
}
public BinaryTree(T data) {
this.root = new BinaryTreeNode(data);
}
//遍历
//先序遍历
public void preTraverse(BinaryTreeNode node){
if(node==null){
return;
}
System.out.printf("%5s",node.data);
preTraverse(node.lchild);
preTraverse(node.rchild);
}
//一个个地插入太麻烦了,我决定写一个按先序遍历 创建二叉树
public BinaryTreeNode preOrderCreateBinaryTree(BinaryTreeNode node,T[] arr) throws IOException {
if(arr[index].equals("*")){
node = null;
index++;
} else{
node = new BinaryTreeNode<T>();
node.data = arr[index];
index++;
node.lchild = preOrderCreateBinaryTree(node.lchild,arr);
node.rchild = preOrderCreateBinaryTree(node.rchild,arr);
}
return node;
}
}
//一个个地插入太麻烦了,我决定写一个按先序遍历 创建二叉树
public BinaryTreeNode preOrderCreateBinaryTree(BinaryTreeNode node,T[] arr) throws IOException {
if(arr[index].equals("*")){
node = null;
index++;
} else{
node = new BinaryTreeNode<T>();
node.data = arr[index];
index++;
//别忘了设置左右孩子的关联
node.lchild = preOrderCreateBinaryTree(node.lchild,arr);
node.rchild = preOrderCreateBinaryTree(node.rchild,arr);
}
//返回修改后的根节点引用
return node;
}测试:
String[] arr = {"11","10","8","5","*","*","9","*","*","*","16","12","*","*","18","*","*"};
String[] arr2 = {"11","10","*","*","12","*","*"};
BinaryTreeNode node = tree2.preOrderCreateBinaryTree(tree2.root, arr);
tree2.preTraverse(node);测试结果:

插入结点:
插入左孩子,如果不存在,则直接插入;如果已存在,则让当前左孩子作为新插入的左孩子的左孩子
(插入右孩子同理)
/**
* 树的结点
* 1. 插入结点:(插入左孩子,如果不存在,则直接插入;如果已存在,则让当前左孩子作为新插入的左孩子的左孩子) (插入右孩子同理)
* @param <T>
*/
public class BinaryTreeNode<T> {
public BinaryTreeNode lchild;
public BinaryTreeNode rchild;
public T data;
public BinaryTreeNode(){
}
public BinaryTreeNode(T data) {
this.lchild = null;
this.rchild = null;
this.data = data;
}
//插入左孩子
public BinaryTreeNode insertLeft( T data){
//判断当前有无左孩子
if(this.lchild==null){
this.lchild = new BinaryTreeNode(data);
}else{ //如果已存在,则让当前左孩子作为新插入的左孩子的左孩子)
BinaryTreeNode oldNode = this.lchild; //保存当前左孩子
BinaryTreeNode newNode = new BinaryTreeNode(data);
this.lchild = newNode;
newNode.lchild = oldNode;
}
return this.lchild;
}
//插入右孩子
public BinaryTreeNode insertRight(T data){
if(this.rchild==null){
this.rchild = new BinaryTreeNode(data);
}else{
BinaryTreeNode oldNode = this.rchild;
BinaryTreeNode newNode = new BinaryTreeNode(data);
this.rchild = newNode;
newNode.rchild = oldNode;
}
return this.rchild;
}
}结果:
/*
* 构造 (按从左到右,层序)
* 11
* 8 16
* 5 9 12 18
* 要在11的左边插入10
*
* 11
* 10 16
* 8 12 18
* 5 9
*
* */测试:
BinaryTree<Integer> tree = new BinaryTree<Integer>(11);
BinaryTreeNode a_node = tree.root;
BinaryTreeNode b_node = a_node.insertLeft(8);
BinaryTreeNode c_node = a_node.insertRight(16);
BinaryTreeNode d_node = b_node.insertLeft(5);
BinaryTreeNode f_node = b_node.insertRight(9);
BinaryTreeNode g_node = c_node.insertLeft(12);
BinaryTreeNode h_node = c_node.insertRight(18);
tree.preTraverse(tree.root);
//插入10
a_node.insertLeft(10);
System.out.println();
tree.preTraverse(tree.root);结果:

//先序遍历
public void preTraverse(BinaryTreeNode node){
if(node==null){
return;
}
System.out.printf("%5s",node.data);
preTraverse(node.lchild);
preTraverse(node.rchild);
}中序,后序同理,用递归实现!
中序
public void inTraverse(BinaryTreeNode node){
if(node==null){
return;
}
inTraverse(node.lchild);
System.out.printf("%5s",node.data);
inTraverse(node.rchild);
}
后序:
public void afterTraverse(BinaryTreeNode node){
if(node==null){
return;
}
afterTraverse(node.lchild);
afterTraverse(node.rchild);
System.out.printf("%5s",node.data);
}即层序遍历
//层序遍历
public void levelTraverse(BinaryTreeNode node) throws Exception {
CycleQueue queue = new CycleQueue(new BinaryTreeNode[100]);
queue.enQueue(node); //初始化,保存根结点
while (!queue.isEmpty()){
BinaryTreeNode current = (BinaryTreeNode) queue.deQueue();
System.out.printf("%5s",current.data); //出队
if(current.lchild!=null){
queue.enQueue(current.lchild);
}
if(current.rchild!=null){
queue.enQueue(current.rchild);
}
}
}总结:
思路:想要做到按层序输出,首先我们发现,层序,是按根 左边孩子,右边孩子,再输出上一个左孩子的左孩子,再输出上一个右孩子的右孩子。
也就是我们在输出的时候,要保存住上一个访问过的左孩子结点,把他们的孩子存储下来,以便以后按序输出
(借助队列来保存,FIFO的特性可以完成这一点:保存将来要输出的左孩子,右孩子,并按序输出)
图:
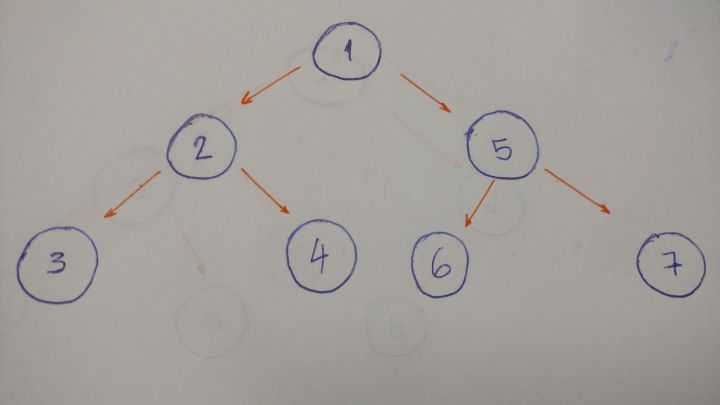
其实:层序:1-2-5-3-4-6-7
我们可以想象成,这个顺序是一条直线,是线性结构:并且先进入的先输出(FIFO)--->并且访问过的要去掉--->
队列
原文:https://www.cnblogs.com/zhanp/p/10932652.html