超市里有N件商品,每个商品都有利润pi和过期时间di,每天只能卖一件商品,过期商品(即当天di<=0)不能再卖。
求合理安排每天卖的商品的情况下,可以得到的最大收益是多少。
输入格式
输入包含多组测试用例。
每组测试用例,以输入整数N开始,接下里输入N对pi和di,分别代表第i件商品的利润和过期时间。
在输入中,数据之间可以自由穿插任意个空格或空行,输入至文件结尾时终止输入,保证数据正确。
输出格式
对于每组产品,输出一个该组的最大收益值。
每个结果占一行。
数据范围
0≤N≤10000,
1≤pi,di≤10000
输入样例:
4 50 2 10 1 20 2 30 1
7 20 1 2 1 10 3 100 2 8 2
5 20 50 10
输出样例:
80
185
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
int main()
{
int n;
while(cin >> n)
{
vector<PII> products(n);
for(int i = 0; i < n; i ++) cin >> products[i].second >> products[i].first; //按时间排序 把时间放在第一个关键字里
sort(products.begin(), products.end()); //排序
priority_queue<int, vector<int>, greater<int>> heap; //小根堆
for(auto p : products) //遍历所有产品
{
heap.push(p.second); //把利润加入
if(heap.size() > p.first) heap.pop();
}
int res = 0;
while(heap.size()) res += heap.top(), heap.pop();
cout << res << endl;
}
return 0;
}给定m个序列,每个包含n个非负整数。
现在我们可以从每个序列中选择一个数字以形成具有m个整数的序列。
很明显,我们一共可以得到nm个这种序列, 然后我们可以计算每个序列中的数字之和,并得到nm个值。
现在请你求出这些序列和之中最小的n个值。
输入格式
第一行输入一个整数T,代表输入中包含测试用例的数量。
接下来输入T组测试用例。
对于每组测试用例,第一行输入两个整数m和n。
接下在m行输入m个整数序列,数列中的整数均不超过10000。
输出格式
对于每组测试用例,均以递增顺序输出最小的n个序列和,数值之间用空格隔开。
每组输出占一行。
数据范围
0<m≤1000,
0<n≤2000
输入样例:
1
2 3
1 2 3
2 2 3
输出样例:
3 3 4
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int>PII; // 存两个数,一个最小值的下标,一个是sum
const int N = 2010;
int m, n; //m行n列
int a[N], b[N], c[N]; //a b 为要合并的序列 c为辅助序列
void merge()
{
priority_queue<PII, vector<PII>, greater<PII>> heap; //小根堆
for(int i = 0; i < n; i++) heap.push({a[0] + b[i], 0}); //b[i] 与a[0] 相加 下标为0
for(int i = 0; i < n; i++)
{
auto t = heap.top();
heap.pop();
int s = t.first, p = t.second; //t为值 p为下标
c[i] = s;
heap.push({s - a[p] + a[p + 1], p + 1});
}
for(int i = 0; i < n; i++) a[i] = c[i];
}
int main()
{
int T;
scanf("%d", &T);
while(T --)
{
scanf("%d%d", &m, &n); //读入行列
for(int i = 0; i < n; i++) scanf("%d", &a[i]); // 读入第一行
sort(a, a + n);
for(int i = 0; i < m - 1; i++) //合并当前序列和下一个序列 合并 m-1 次
{
for(int j = 0; j < n; j ++) scanf("%d", &b[j]);
merge(); //合并a和b 然后把结果存进a
}
for(int i = 0; i < n; i++) printf("%d ", a[i]);
puts("");
}
return 0;
}在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。
可以先将1、2堆合并,新堆数目为3,耗费体力为3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为12。
所以达达总共耗费体力=3+12=15。
可以证明15为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数n,表示果子的种类数。
第二行包含n个整数,用空格分隔,第i个整数ai
是第i种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
输入数据保证这个值小于231。
数据范围
1≤n≤10000,
1≤ai≤20000
输入样例:
3
1 2 9
输出样例:
15
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
priority_queue<int, vector<int>, greater<int>> heap; //小根堆
for(int i = 0; i < n; i++)
{
int x;
cin >> x;
heap.push(x);
}
int res = 0;
while(heap.size() > 1) //小根堆有两个元素 合并最小的两个数
{
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
res += a + b;
heap.push(a + b);
}
cout << res << endl;
return 0;
}追逐影子的人,自己就是影子。 ——荷马
达达最近迷上了文学。
她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。
但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了,达达想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 n 种不同的单词,从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。
达达想要用 k 进制串 si来替换第 i 种单词,使得其满足如下要求:
对于任意的 1≤i,j≤n,i≠j,都有:si不是 sj的前缀。
现在达达想要知道,如何选择 si,才能使替换以后得到的新的《荷马史诗》长度最小。
在确保总长度最小的情况下,达达还想知道最长的 si的最短长度是多少?
一个字符串被称为 k 进制字符串,当且仅当它的每个字符是 0 到 k?1 之间(包括 0 和 k?1)的整数。
字符串 Str1 被称为字符串 Str2 的前缀,当且仅当:存在 1≤t≤m,使得 Str1=Str2[1..t]。
其中,m 是字符串 Str2 的长度,Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串。
输入格式
输入文件的第 1 行包含 2 个正整数 n,k,中间用单个空格隔开,表示共有 n 种单词,需要使用 k 进制字符串进行替换。
第2~n+1 行:第 i+1 行包含 1 个非负整数 wi,表示第 i 种单词的出现次数。
输出格式
输出文件包括 2 行。
第 1 行输出 1 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数,为保证最短总长度的情况下,最长字符串 si的最短长度。
数据范围
2≤n≤100000,
2≤k≤9
输入样例:
4 2
1
1
2
2
输出样例:
12
2
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
int main()
{
int n, k;
cin >> n >> k;
priority_queue<PLI, vector<PLI>, greater<PLI>> heap; //小根堆
for(int i = 0; i < n; i++)
{
LL x; //输入值 LL
cin >> x;
heap.push({x, 0}); //将x插入优先队列里面 下标最开始高度是0
}
while((n - 1) % (k - 1)) heap.push({0, 0}), n++; // (n-1)%(k-1) != 0 往里面添加0
LL res = 0;
while(heap.size() > 1)
{
LL s = 0;
int depth = 0; //新节点深度
for(int i = 0; i < k; i ++) //取出最小的k个
{
auto t = heap.top();
s += t.first; //权值
depth = max(depth, t.second);
heap.pop();
}
res += s;
heap.push({s, depth + 1}); //父节点 高1
}
cout << res << endl << heap.top().second << endl;
return 0;
}你在一家IT公司为大型写字楼或办公楼的计算机数据做备份。
然而数据备份的工作是枯燥乏味的,因此你想设计一个系统让不同的办公楼彼此之间互相备份,而你则坐在家中尽享计算机游戏的乐趣。
已知办公楼都位于同一条街上,你决定给这些办公楼配对(两个一组)。
每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。
然而,网络电缆的费用很高。
当地电信公司仅能为你提供 K 条网络电缆,这意味着你仅能为 K 对办公楼(总计2K个办公楼)安排备份。
任意一个办公楼都属于唯一的配对组(换句话说,这 2K 个办公楼一定是相异的)。
此外,电信公司需按网络电缆的长度(公里数)收费。
因而,你需要选择这 K 对办公楼使得电缆的总长度尽可能短。
换句话说,你需要选择这 K 对办公楼,使得每一对办公楼之间的距离之和(总距离)尽可能小。
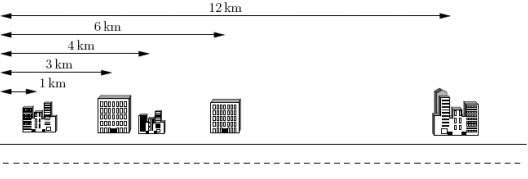
下面给出一个示例,假定你有 5 个客户,其办公楼都在一条街上,如下图所示。
这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。
电信公司仅为你提供 K=2 条电缆。
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连,第 3 个和第 4 个办公楼相连。
这样可按要求使用 K=2 条电缆。
第 1 条电缆的长度是 3km-1km=2km ,第 2 条电缆的长度是 6km-4km=2km。
这种配对方案需要总长 4km 的网络电缆,满足距离之和最小的要求。
输入格式
第一行输入整数n和k,其中 n 表示办公楼的数目,k 表示可利用的网络电缆的数目。
接下来的n行每行仅包含一个整数s,表示每个办公楼到大街起点处的距离。
这些整数将按照从小到大的顺序依次出现。
输出格式
输出应由一个正整数组成,给出将2K个相异的办公楼连成k对所需的网络电缆的最小总长度。
数据范围
2≤n≤100000,
1≤k≤n/2,
0≤s≤1000000000
输入样例:
5 2
1
3
4
6
12
输出样例:
4
#include <iostream>
#include <queue>
#include <vector>
#include <set>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 100010;
int n, k; // n 表示办公楼的数目,k 表示可利用的网络电缆的数目
int l[N], r[N]; //双向链表左指针 右指针
LL d[N]; //d是差值
void delete_node(int p)
{
r[l[p]] = r[p]; //左边的右指针 = 右边
l[r[p]] = l[p]; //右边的左指针 = 左边
}
int main()
{
cin >> n >> k;
for(int i = 0; i < n; i ++) cin >> d[i];
for(int i = n - 1; ~i; i --) d[i] -= d[i - 1]; //当前与前一位的差值
set<PLI> S; //需要动态修改 堆 用 set
d[0] = d[n] = 1e15; //处理边界问题 定义两个哨兵
for(int i = 0; i <= n; i ++)
{
l[i] = i - 1;
r[i] = i + 1;
if( i >= 1 && i < n) S.insert({d[i], i}); // push 值和下标
}
LL res = 0;
while(k --)
{
auto it = S.begin(); //s里的最小值
LL v = it->first; //值
int p = it->second, left = l[p], right = r[p]; //下标 左儿子 右儿子
S.erase(it);
S.erase({d[left], left}), S.erase({d[right], right});//从平衡树删掉
delete_node(left), delete_node(right); //删除左右两边的点
res += v;
d[p] = d[left] + d[right] - d[p];
S.insert({d[p], p});
}
cout << res << endl;
return 0;
}原文:https://www.cnblogs.com/wmxnlfd/p/10935393.html