一:位运算符详解
位运算符主要用来对操作数二进制的位进行运算。按位运算表示按每个二进制位(bit)进行计算,其操作数和运算结果都是整型值。
Java 语言中的位运算符分为位逻辑运算符和位移运算符两类,下面详细介绍每类包含的运算符。
1,位逻辑运算符
位逻辑运算符包含 4 个:&(与)、|(或)、~(非)和 ^(异或)。除了 ~(即位取反)为单目运算符外,其余都为双目运算符。表 1 中列出了它们的基本用法。
| 运算符 | 含义 | 实例 | 结果 |
|---|---|---|---|
| & | 按位进行与运算 | 4 & 5 | 4 |
| | | 按位进行或运算 | 4 | 5 | 5 |
| ^ | 按位进行异或运算 | 4 ^ 5 | 1 |
| ~ | 按位进行取反运算 | ~ 4 | -5 |
位与运算符为 &,其运算规则是:参与运算的数字,低位对齐,高位不足的补零,如果对应的二进制位同时为 1,那么计算结果才为 1,否则为 0。因此,任何数与 0 进行按位与运算,其结果都为 0。
例如下面的表达式:
100&0
图 1 所示为这个运算过程,结果为 0。
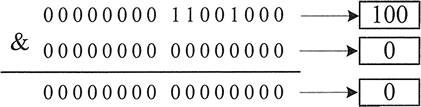
下面是两个非零的数字进行位与运算的过程。
这两行语句执行后变量 Z 的值是 4,图 2 所示为这个运算过程。
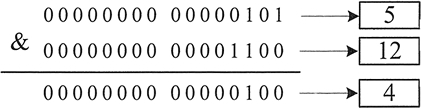
位或运算符为 |,其运算规则是:参与运算的数字,低位对齐,高位不足的补零。如果对应的二进制位只要有一个为 1,那么结果就为 1;如果对应的二进制位都为 0,结果才为 0。
下面是一个使用位或运算符的表达式。
11|7
运算结果为 15,图 3 所示为其运算过程。
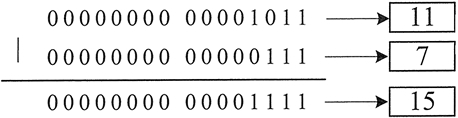
位异或运算符为 ^,其运算规则是:参与运算的数字,低位对齐,高位不足的补零,如果对应的二进制位相同(同时为 0 或同时为 1)时,结果为 0;如果对应的二进制位不相同,结果则为 1。
下面是一个使用位异或运算符的表达式。
11^7
运算结果为 12,图 4 所示为其运算过程。
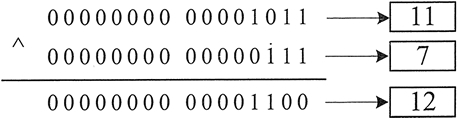
提示:在有的高级语言中,将运算符 ^ 作为求幂运算符,要注意区分。
位取反运算符为 ~,其运算规则是:只对一个操作数进行运算,将操作数二进制中的 1 改为 0,0 改为 1。
下面是一个使用位取反运算符的表达式。
~10
运算结果为 65525,图 5 所示为其运算过程。
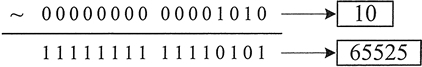
我们可以使用如下的程序来检查这个运算结果。
编译执行以上程序,会发现输出的结果是 -11,而不是 65525。这是因为取反之后的结果是十六进制数,而在上面的程序中使用 %d 将输出转换为了十进制数。
可以使用如下语句查看十六进制结果。
可以看到输出结果为 fff5,将它转换为二进制是 1111111111110101。这个二进制数的最高位为 1,表示这个数为负数。除最高位外,按位取反再加 1,即得到二进制原码 1000000000001011,用十进制数表示即为 -11。
注意:位运算符的操作数只能是整型或者字符型数据以及它们的变体,不用于 float、double 或者 long 等复杂的数据类型。
2,位移运算符
位移运算符用来将操作数向某个方向(向左或者右)移动指定的二进制位数。表 2 列出了 Java 语言中的两个位移运算符,它们都属于双目运算符。
| 运算符 | 含义 | 实例 | 结果 |
|---|---|---|---|
| » | 右移位运算符 | 8»1 | 4 |
| « | 左移位运算符 | 9«2 | 36 |
左移位运算符为 «,其运算规则是:按二进制形式把所有的数字向左移动对应的位数,高位移出(舍弃),低位的空位补零。
例如,将整数 11 向左位移 1 位的过程如图 6 所示。
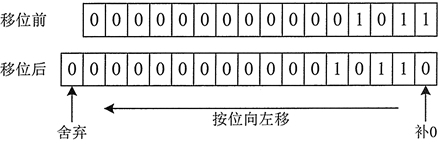
从图 6 中可以看到,原来数的所有二进制位都向左移动 1 位。原来位于左边的最高位 0 被移出舍弃,再向尾部追加 0 补位。最终到的结果是 22,相当于原来数的 2 倍。
右位移运算符为 »,其运算规则是:按二进制形式把所有的数字向右移动对应的位数,低位移出(舍弃),高位的空位补零。
例如,将整数 11 向右位移 1 位的过程如图 7 所示。
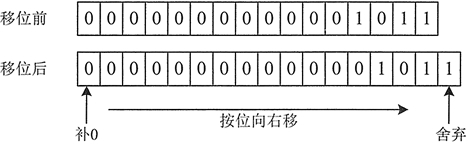
从图 7 中可以看到,原来数的所有二进制位都向右移动 1 位。原来位于右边的最低位 1 被移出舍弃,再向最高位追加 0 补位。最终到的结果是 5,相当于原数整除 2 的结果。
---------详解部分------------
作者:http://c.biancheng.net
来源:http://c.biancheng.net
原文:http://c.biancheng.net/view/784.html
版权声明:本文为博主原创文章,转载请附上博文链接!
二:位运算符妙用
位运算作为底层的基本运算操作,往往是和‘高效‘二字沾边,适当的运用位运算来优化系统的核心代码,会让你的代码变得十分的精妙。以下是我所遇之的一些简单的位运算技巧作为博文记录。
1.获得int型最大值
public static void main(String[] args) {
int maxInt = (1 << 31) - 1;
int maxInt1 = ~(1 << 31);
int maxInt2 = (1 << -1) - 1;
int maxInt3 = (-1>>>1);
System.out.println("十进制: "+ maxInt +" ,二进制: " + Integer.toBinaryString(maxInt));
System.out.println("十进制: "+ maxInt1 +" ,二进制: " + Integer.toBinaryString(maxInt1));
System.out.println("十进制: "+ maxInt2 +" ,二进制: " + Integer.toBinaryString(maxInt2));
System.out.println("十进制: "+ maxInt3 +" ,二进制: " + Integer.toBinaryString(maxInt3));
}
/** ~output~
十进制: 2147483647 ,二进制: 1111111111111111111111111111111
十进制: 2147483647 ,二进制: 1111111111111111111111111111111
十进制: 2147483647 ,二进制: 1111111111111111111111111111111
十进制: 2147483647 ,二进制: 1111111111111111111111111111111
*/
exp:int类型为32位,要获得int的最大值,只需要最高位为0(正数),其余位为1,便可得到最大数[01111111 11111111 11111111 11111111](2进制)、[0xFFFFFFF](16进制)。
2.获得int型最小值
public static void main(String[] args) {
int minInt = 1 << 31;
int minInt1 = -1 << 31;
int minInt2 = 1 << -1;
System.out.println("十进制: "+ minInt +" ,二进制: " + Integer.toBinaryString(minInt));
System.out.println("十进制: "+ minInt1 +" ,二进制: " + Integer.toBinaryString(minInt1));
System.out.println("十进制: "+ minInt2 +" ,二进制: " + Integer.toBinaryString(minInt2));
System.out.println("十进制: "+ 0x80000000 +" ,二进制: " + Integer.toBinaryString(0x80000000));
}
/** ~output~
十进制: -2147483648 ,二进制: 10000000000000000000000000000000
十进制: -2147483648 ,二进制: 10000000000000000000000000000000
十进制: -2147483648 ,二进制: 10000000000000000000000000000000
十进制: -2147483648 ,二进制: 10000000000000000000000000000000
*/
exp:int类型为32位,要获得int的最大值,只需要最高位为1(负数),其余位为0,便可得到最大数[10000000 00000000 00000000 00000000](2进制)、[0x80000000](16进制)。
负数最小二进制和正数最大二进制似乎有很大区别,这是因为cpu中只有加法器,减法只是加法的一种形式,而计算机是如何通过加法来计算减法的呢?
计算机对负数的实际表示是补码形式,补码的计算是以负数绝对值的原码(二进制)取反[不操作符号位],再加1得到,举个例子:
-7 的绝对值原码(二进制) = 1 000 0111 # 最高位为负数标记
1 000 0111取反 1 111 1000 # 符号位不取反
取反后加1 = 1 111 1000 + 1 = 1 111 1001 # 则得到-7的补码 1 111 1001
计算 6 - 7 = 6 + (-7) = 0 000 0110 + 1 111 1001 = 1 111 1111
可以看到得到的结果为1 111 1111 最高位为1 ,结果为负数,是补码的形式。我们反向推理,1 111 1111 - 1 = 1111 1110,取反(最高位符号位不操作) 1 111 1110取反得到原码1 000 0001,所以可知十进制值 -1。
3.乘以2的m次方或除以2的m次方
// 计算n*(2^m)
public static int mulTwoPower(int n,int m){
return n << m;
}
// 计算n/(2^m)
public static int divTwoPower(int n,int m){
return n >> m;
}
public static void main(String[] args) {
System.out.println("5 * 2 * 2 * 2 = "+ mulTwoPower(5, 3) );
System.out.println("6 / 2 / 2 = "+ divTwoPower(6, 2) );
}
/** ~output~
5 * 2 * 2 * 2 = 40
6 / 2 / 2 = 1
*/
我们知道十进制是逢十进一,二进制是逢二进一 ,十进制*10,扩大原来的10倍,尾部多一个0,二进制*2,扩大原来的2倍,尾数也多一个0,这便相当于二进制数左移<<1位,0000 1111 * 2 = 0001 1110, 除以2则反之。
4.判断奇偶数
// true 奇数 false 偶数
public static boolean isOddNumber(int n){
return (n & 1) == 1;
}
public static void main(String[] args) {
System.out.println("5 是 "+ isOddNumber(5) );
System.out.println("1234 是 "+ isOddNumber(1234) );
}
/** ~output~
5 是 true
1234 是 false
*/
这里知识是二进制最尾部的尾数为1,则此数必为奇数,尾数为0,此数必为偶数。所以通过与运算便可确定这个数的奇偶性。
5.对2的n次方取余
public static int indexFor(int m, int n){
return m & (n - 1);
}
public static void main(String[] args) {
System.out.println("19 与 16 求余 = "+ indexFor(19, 16) );
System.out.println("19 与 16 求余 = "+ 19 % 16 );
}
/** ~output~
19 与 16 求余 = 3
19 与 16 求余 = 3
*/
此方法中n为2的指数值,则其二进制形式的表示中只存在一个1,其余位都为0,例如: 0000 1000、0100 0000、0010 0000等等。
则n-1的二进制形式就为1的位数变为0,其右边位全变为1,例如16的二进制 0001 0000 -1 = 0000 1111
测试m为19的二进制 0001 0011 & 0000 1111 = 0000 0011 = 3,地位保留的结果便是余数。
此位运算也是HashMap中确定元素键(key)值所在哈希数组下标位置的核心方法,此位运算(hash & (length - 1))的效率极高于hash % length的求余, 所以也解释了为什么HashMap的扩容始终为2的倍数(2的指数值)。
6.快速幂算法,求n的m次方
// 快速幂算法求n的m次方
public static int power(int n, int m) {
int temp = 1, base = n;
while (m != 0) {
if ((m & 1) == 1) { // 判断奇偶,
temp = temp * base;
}
base = base * base;
m >>= 1; // 舍弃尾部位
}
return temp;
}
public static void main(String[] args) {
System.out.println("3的3次方 = " + power(3,3));
System.out.println("5的7次方 = " + power(5,7));
}
/** ~output~
3的3次方 = 27
5的7次方 = 78125
*/
我们知道,求n的m次方最简单暴力的方法是循环m次求n的乘积,如今的计算机非常强大,这方面的性能似乎完全可以忽略优化,但对于微型机来说,代码优化应该是你时时刻刻需要考虑的,我们也从另外的问题出发:如何使用更少的时间复杂度去实现n的m次方呢?
快速幂算法,下面来看下他的实现原理。
在数学中,存在等式n^m = n^(m1+m2+m3+.....+mk) = n^m1 * n^m2 * n^m3 * ...* n^mk, 且m1 + m2 + m3 +....+mk = m
我们计算m的二进制,如上示例幂数7的二进制=0000 0111,他的十进制计算为: 1+2+4,所以5^7 = 5^(1+2+4) = 5^1 * 5^2 * 5^4,可以看出时间复杂度为f(n)=lgn
---------妙用部分------------
作者:我叫lilee
来源:CSDN
原文:https://blog.csdn.net/minaki_/article/details/81980079
版权声明:本文为博主原创文章,转载请附上博文链接!
原文:https://www.cnblogs.com/ruanian/p/10936154.html