前传
这题真的hin简单,真的
前言
这是一道看上去不是毒瘤但实际上有那么一seisei毒瘤的题目
在我多次提交代码仍然屡教不改最后痛改前非的惨痛经历下,总结出以下#¥@¥#%:
1.不要用结构体存 a , b
2.多取模,越多越好,能往哪里mod就往哪里mod
(一开始mod少了,然后就Wa了)

解析
1. 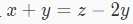 把这个式子化简一下
把这个式子化简一下
z - x = 3 y
也就是说明 z,x 属于同一个mod(3)的剩余类
如果 z 是 15 的话,那么 x 可以是 3 6 9 12 (%3……0)
如果 z 是 16 的话,那么 x 可以是 1 4 7 10 (%3…… 1)
如果 z 是 17 的话,那么 x 可以是 2 5 8 11 (%3…… 2)
所以我们就可以枚举 z ,那么符合条件的 x 就是和它同属一个剩余类并且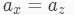 的啦
的啦
2. 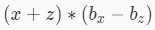 我们把这个式子拆一下
我们把这个式子拆一下
( x + z )·( bx - bz )
= x·bx + z·bx - x·bz - z·bz
所以说,对于每一个 z ,它可以有很多个对应的 x ,虽然 x ,bx 不确定,但是 z , bz 是确定的
也就是说对于每一个 z 都可以得到以下这个式子
∑( x·bx ) + z·∑bx - bz·∑x - z·bz·(z的个数)
从前往后枚举 z ,对于每一个 z ,可以满足这个 z 要求的 x 一定也可以满足下一个和这个 z 相类似的 z ,所以说我们就开数组统计一下
S[ ] 到当前为止的满足 z 的 x 的数目
Sx[ ] 到当前为止的满足 z 的 x 的和
Sbx[ ] 到当前为止的满足 z 的 bx 的和
Sxbx[ ] 到当前为止的满足 z 的 x*bx 的和
每次先统计,再更新数组
对于代码当中呢,是枚举三种剩余类,也就是 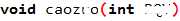
每次操作之前都要初始化一下
然后开始 for 循环枚举 z ,计算 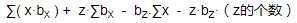
然后更新数组,按照 a 的种类更新到数组中的不同地方,数组中每一个小格子代表一个种类的桶
注意保证答案不为负数 貌似取模就已经保证了
最后输出答案即可
代码
#include<bits/stdc++.h> using namespace std; const int mod=10007; const int maxn=100001; int n,m; long long ans; int S[maxn],Sx[maxn],Sbx[maxn],Sxbx[maxn]; int a[maxn],b[maxn]; void caozuo(int RQY) { long long hxbx,hzbx,hbzx,hzbz; int num=0; memset(S,0,sizeof(S)); memset(Sx,0,sizeof(Sx)); memset(Sbx,0,sizeof(Sbx)); memset(Sxbx,0,sizeof(Sxbx)); for(int i=RQY;i<=n;i+=3) { num=a[i] ; hxbx=Sxbx[num]; hzbx=i%mod*Sbx[num]%mod; hbzx=Sx[num]%mod*b[i]%mod ; hzbz=i%mod*b[i]%mod*S[num]%mod ; ans=(ans+hxbx+hzbx-hbzx-hzbz)%mod; S[num]++; Sx[num]=(Sx[num]%mod+i%mod)%mod; Sbx[num]=(Sbx[num]%mod+b[i]%mod)%mod; Sxbx[num]=(Sxbx[num]%mod+(i%mod*b[i]%mod))%mod; } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&b[i]); for(int i=1;i<=n;i++) scanf("%d",&a[i]); caozuo(1); caozuo(2); caozuo(3); while(ans<0) { ans+=mod; } printf("%ld",ans%mod); return 0; }
~~~~~~QWQ写完之后我发现我要好好组织语言~~~~~~
原文:https://www.cnblogs.com/xiaoyezi-wink/p/10946228.html