当信道确定时,\(I(X;Y)?\)是\(p(a_i)(i = 1,...,r)?\)的函数,这是一个多元函数,并且
\[
\sum_{i=1}^rp(a_i) = 1
\]
根据求多元函数极值的方法,我们构建辅助函数
\[
F[p(a_1), ... , p(a_r), \lambda] = I(X;Y) - \lambda[\sum_{i=1}^r p(a_i) - 1]
\]
则要使得\(I(X;Y)\)在条件\(\sum\limits_{i=1}^rp(a_i) = 1\)下取得极值,需要满足
\[
\begin{aligned}
&\cfrac{\partial F}{\partial p(a_i)} = \cfrac{\partial \{I(X;Y) - \lambda[\sum\limits_{i = 1}^{r}p(a_i) - 1]\}}{\partial p(a_i)} = 0 \&\sum_{i=1}^rp(a_i) = 1
\end{aligned}
\]
经过复杂的数学计算,我们得到
\[
\begin{aligned}
&\sum_{j=1}^{s}p(b_j/a_i)\ln\cfrac{p(b_j/a_i)}{p(b_j)} = \lambda + 1\&\sum_{i=1}^rp(a_i) = 1
\end{aligned}
\]
对第一个式子乘以\(p(a_i)\)并对\(i\)求和
\[
\sum_{i = 1}^{r}\sum_{j=1}^{s}p(a_i)p(b_j/a_i)\ln\cfrac{p(b_j/a_i)}{p(b_j)} = \sum_{i=1}^{r}p(a_i)(\lambda + 1)
\]
上式的左边即为信道容量\(C\)的表达式,所以
\[
C = \lambda + 1
\]
所以我们又可以得到
\[
\sum_{j=1}^{s}p(b_j/a_i)\ln\cfrac{p(b_j/a_i)}{p(b_j)} = C
\]
进行化简可以得到
\[
\sum_{j = 1}^{s}p(b_j/a_i)[C + \ln p(b_j)] = \sum_{j = 1}^{s}p(b_j/a_i)\ln p(b_j/a_i)
\]
令
\[
\beta_j = C + \ln p(b_j)
\]
得到
\[
\sum_{j = 1}^{s}p(b_j/a_i)\beta_j = \sum_{j = 1}^{s}p(b_j/a_i)\ln p(b_j/a_i)
\]
这是一个关于\(\beta_j\)的方程组,可以求出\(\beta_j\),根据\(C\)与\(\beta_j\)的关系,我们得到
\[
C = \ln\{\sum_{j = 1}^{s}e^{\beta_j}\}
\]
根据求得的\(C\)和\(\beta_j\),代入
\[
\beta_j = C + \ln p(b_j)
\]
可以求得\(p(b_j)\),然后根据
\[
p(b_j) = \sum_{i = 1}^{r}p(a_i)p(b_j/a_i)
\]
可以解出\(p(a_i)\),即得到了使\(I(X;Y)\)最大的信源概率分布。
该种信道的特点是,其信道概率矩阵每列只有一个非零的数,如下
\[
\begin{array}{*{20}{l}}
{\quad \quad \quad \qquad \quad {b_1}\qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b_2}\qquad \qquad {b_3}\qquad \qquad {b_4}\qquad \qquad {b_5}\qquad \qquad {b_6}\qquad \qquad {b_7}}\{[P] = \begin{array}{*{20}{c}}
{{a_1}}\{{a_2}}\{{a_3}}\{{a_4}}
\end{array}\left( {\begin{array}{*{20}{c}}
{p({b_1}/{a_1})}&{p({b_2}/{a_1})}&0&0&0&0&0\0&0&{p({b_3}/{a_2})}&{p({b_4}/{a_2})}&{p({b_5}/{a_2})}&0&0\0&0&0&0&0&{p({b_6}/{a_3})}&0\0&0&0&0&0&0&{p({b_7}/{a_4})}
\end{array}} \right)}
\end{array}
\]
对应的模型为
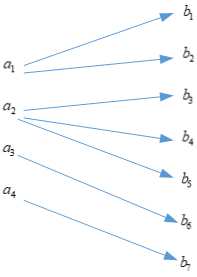
此时
\[
I(X;Y) = H(X) - H(X|Y) = H(X)
\]
根据信道容量的定义,则
\[
C = max\{I(X;Y)\} = max\{H(X)\} = \log r
\]
当信源概率分布等概时取等号。
该信道的特点是,其信道概率矩阵只由\(0\)或\(1?\)组成
\[
\begin{array}{l}
\qquad \quad \quad\,\,{\mkern 1mu} {\mkern 1mu} {b_1}\,\,\,\, {b_2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\,\, {b_3}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\, {b_4}\P = \begin{array}{*{20}{c}}
{{a_1}}\{{a_2}}\{{a_3}}\{{a_4}}\{{a_5}}\{{a_6}}\{{a_7}}
\end{array}\left( {\begin{array}{*{20}{c}}
1&0&0&0\0&0&1&0\0&1&0&0\0&0&0&1\1&0&0&0\0&0&1&0\0&1&0&0
\end{array}} \right)
\end{array}
\]
对应的模型为
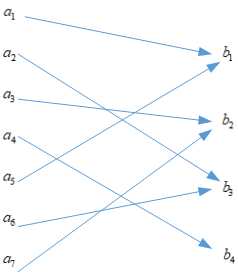
此时
\[
I(X;Y) = H(Y) - H(Y|X) = H(Y)
\]
则
\[
C = max\{H(Y)\} = \log s
\]
当输出变量\(Y\)等概分布时得到,那么信源\(X\)的分布是什么才能使输出\(Y\)等概分布呢? 其实匹配的信源并不是唯一的。
我们定义强对称信道的信道概率矩阵为
\[
\begin{array}{l}
\qquad\qquad\quad\quad{a_i}\quad\quad\quad{a_2} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\quad\,\, \cdots \qquad {a_r}\[P] = \begin{array}{*{20}{c}}
{{a_1}}\{{a_2}}\ \vdots \{{a_r}}
\end{array}\left[ {\begin{array}{*{20}{c}}
{(1 - \epsilon)}&{\cfrac{\epsilon}{{r - 1}}}& \cdots &{\cfrac{\epsilon}{{r - 1}}}\{\cfrac{\epsilon}{{r - 1}}}&{(1 - \epsilon)}& \cdots &{\cfrac{\epsilon}{{r - 1}}}\ \vdots & \vdots & \cdots & \vdots \{\cfrac{\epsilon}{{r - 1}}}&{\cfrac{\epsilon}{{r - 1}}}& \cdots &{(1 - \epsilon)}
\end{array}} \right]
\end{array}
\]
输入随机变量\(X\)和输出随机变量\(Y\)的符号数均为\(r\),每一个输入符号的总的错误传递概率为\(\epsilon?\)的强对称信道。它的信道容量的求法如下
\[
\begin{aligned}
H(Y|X) &= -\sum_{i=1}^{r}\sum_{j=1}^{r} p(a_i)p(a_j/a_i) \log p(a_j/a_i) \&= ... \&=H(\epsilon) + \epsilon \log(r-1)
\end{aligned}
\]
则
\[
C = max\{I(X;Y)\} = max\{H(Y) - H(Y|X)\} = \log r - H(\epsilon) - \epsilon \log(r - 1)
\]
当输出\(Y\)等概时取得等号,那个信源\(X\)什么分布会使得输出\(Y\)等概,答案是\(X\)等概,所以我们得到这么一个结论,对于强对称信道,当信源分布等概时,此时\(I(X;Y)\)取得最大值为
\[
C = \log r - H(\epsilon) - \epsilon\log(r-1)
\]
原文:https://www.cnblogs.com/LastKnight/p/10951732.html