线段树扫描线的应用
我们尝试设想有一条无限高的竖线左往右扫过这个并集图形,按照每一个矩形的的左右边界,我们可以将这个并集图形分为2n 段,对于两两相邻的部分,我们可以分别计算面积,这样就得到了整个并集图形的面积。
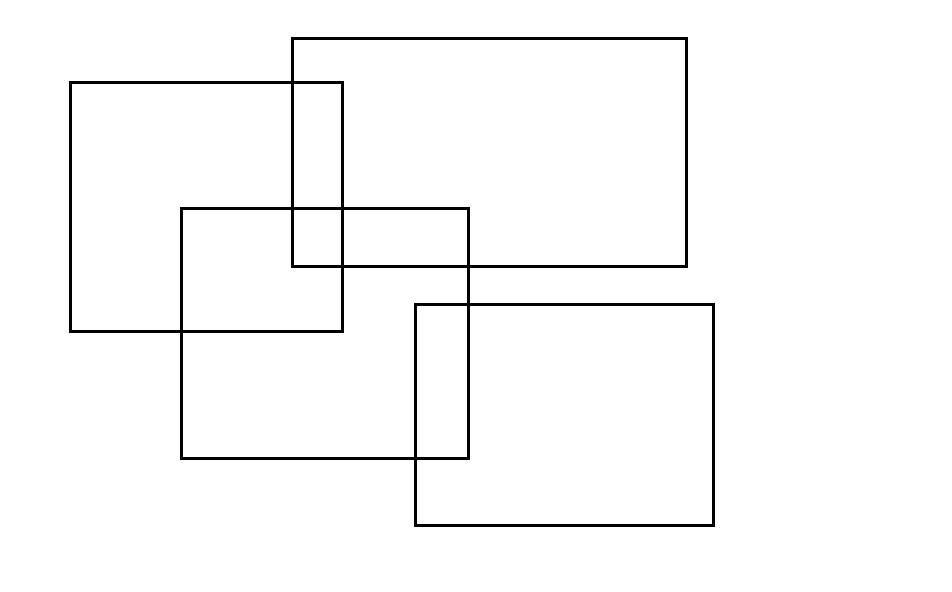
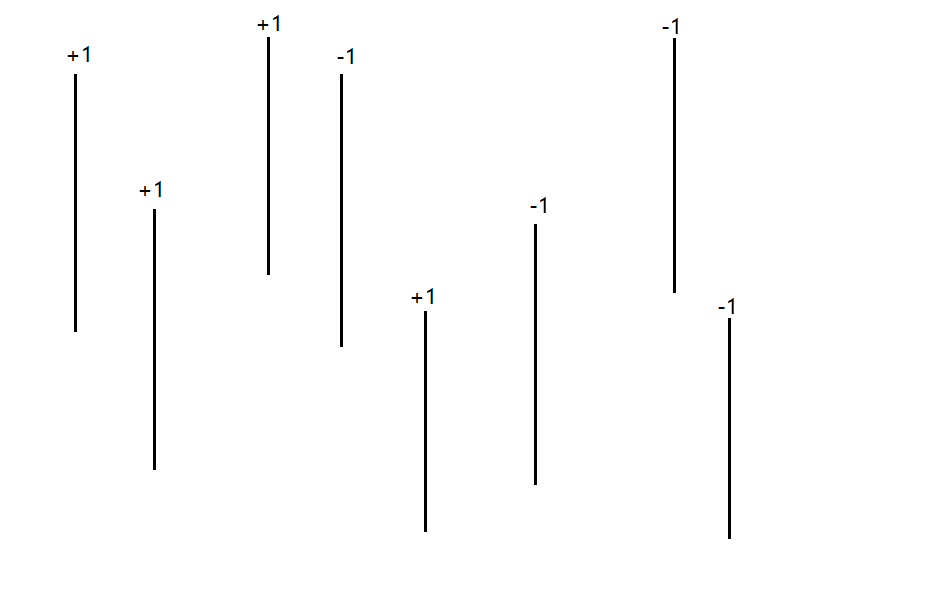
如图,我们就是把每个矩形的左右边界提了出来,就变成了这样一些线段。
那么我们需要这些量化记录下来:每个四元组(x,y1,y2,1/−1)分别代表了一条线段,x是线段的横坐标,(y1,y2)是线段上下端点的纵坐标,1/−1代表了这条线段是矩形的左边界还是右边界。
显然,我们只需要把这些线段按照横坐标排序,对于一次遍历来说,两两线段之间的距离是已知的。那么我们需要解决的问题就是纵坐标的影响范围。
我们不妨把纵坐标都取出来,离散化映射到[1,T]之间的T个整数值,并将这些纵坐标表示为T−1段,其中第i段代表了第i个纵坐标和第i+1个纵坐标之间的部分,然后,我们设立数组ci代表第i段被覆盖的次数。
这样,我们就可以用如下的算法流程计算矩形的面积:
1. 对于每一个线段,将其的k值累加到这个线段对应的若干个纵坐标区间
2. 计算面积:所有T−1个纵坐标区间对应的c值大于零的就说明这些部分的区间还存在,将存在的区间的长度累加起来,乘上当前线段与下一条线段之间的横坐标之差就是这两条线段之间的面积。
显然,这里需要我们维护一个区间内的区间加法,区间求和,这个就是线段树的事情了。
由于本题中的区间修改成对出现,互相抵消,所以我们可以不写带有lazytag的线段树。我们在线段树的每一个节点上维护两个值cnt和len,cnt代表这段区间被覆盖的次数,如果cnt>0则当前区间的len等于当前区间的纵坐标长度,反之lenp=lenp∗2+lenp∗2+1。那么对于每一次区间修改,我们直接在线段树上改cnt的值即可,并沿路更新len值即可。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 typedef long long ll; 7 struct line { 8 double x,y1,y2; 9 int f; 10 bool operator <(const line &xx) const { 11 return x<xx.x; 12 } 13 }a[120<<1]; 14 struct node { 15 int l,r; 16 double cnt,len; 17 }s[120<<3]; 18 int n,t,T,val[120<<1][2]; 19 double raw[120<<1],ans; 20 inline void build(int now,int l,int r) { 21 s[now].l=l; s[now].r=r; 22 if(l==r) return ; 23 int mid=l+r>>1; 24 build(now<<1,l,mid); 25 build(now<<1|1,mid+1,r); 26 } 27 inline void pushup(int now) { 28 if(s[now].cnt>0) s[now].len=raw[s[now].r+1]-raw[s[now].l]; 29 else if(s[now].l==s[now].r) s[now].len=0; 30 else s[now].len=s[now<<1].len+s[now<<1|1].len; 31 } 32 void updata(int now,int l,int r,int v) { 33 if(l<=s[now].l&&s[now].r<=r) { 34 s[now].cnt+=v; 35 pushup(now); 36 return ; 37 } 38 int mid=s[now].l+s[now].r>>1; 39 if(l<=mid) updata(now<<1,l,r,v); 40 if(r>mid) updata(now<<1|1,l,r,v); 41 pushup(now); 42 } 43 int main() { 44 while(cin>>n&&n) { 45 ans=t=0; 46 for(int i=1;i<=n;i++) { 47 double x1,x2,y1,y2; 48 cin>>x1>>y1>>x2>>y2; 49 a[2*i-1]=(line){x1,y1,y2,1}; 50 a[2*i]=(line){x2,y1,y2,-1}; 51 raw[++t]=y1; 52 raw[++t]=y2; 53 } 54 sort(a+1,a+2*n+1); 55 sort(raw+1,raw+t+1); 56 t=unique(raw+1,raw+t+1)-(raw+1); 57 for(int i=1;i<=2*n;i++) { 58 val[i][0]=lower_bound(raw+1,raw+t+1,a[i].y1)-raw; 59 val[i][1]=lower_bound(raw+1,raw+t+1,a[i].y2)-raw; 60 } 61 build(1,1,t); 62 for(int i=1;i<=2*n;i++) { 63 updata(1,val[i][0],val[i][1]-1,a[i].f); 64 ans+=(a[i+1].x-a[i].x)*s[1].len; 65 } 66 printf("Test case #%d\nTotal explored area: %.2lf\n\n",++T,ans); 67 } 68 return 0; 69 }
原文:https://www.cnblogs.com/shl-blog/p/10958035.html