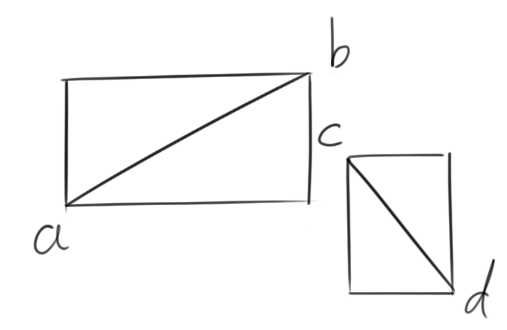
1 bool quick_judge(point a,point b,point c,point d) 2 { 3 if(a.y>c.y||b.y<d.y||a.x>d.x||b.x<c.x) 4 return false; 5 else return true; 6 }
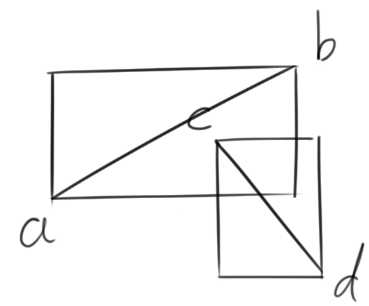
但是仅这一种判断方式无法解决我们的问题,有反例如下图,两矩形相交但是线段并没有相交,这就需要我们用第二种方法来加以辅助。
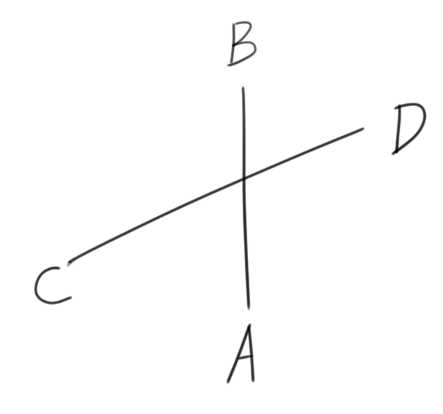
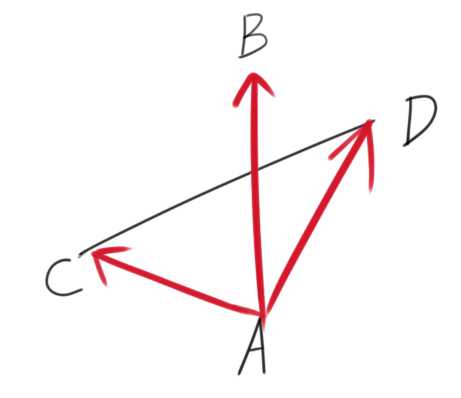
1 bool cross_judge(point a,point b,point c,point d) 2 { 3 const double eps=1e-9; 4 double ac,ad,cb,ca; 5 ac=(c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x); 6 ad=(d.x-a.x)*(b.y-a.y)-(d.y-a.y)*(b.x-a.x); 7 ca=(a.x-c.x)*(d.y-c.y)-(a.y-c.y)*(d.x-c.x); //保险起见,把另一条边也判断一下 8 cb=(b.x-c.x)*(d.y-c.y)-(b.y-c.y)*(d.x-c.x); 9 if(ac*ad<eps&&ca*cb<eps) return true; 10 else return false; 11 }
至此,我们将这两个方法结合一下,就可以解决我们的问题了。
原文:https://www.cnblogs.com/CSGOBESTGAMEEVER/p/10939868.html