其实圆周运算是针对周期序列而言的,由于周期序列在每一个周期内的取值都相同,所以我们只关注它的主值区间,比如,如果一个序列的长度为\(N\)的话,那么它的主值区间就是\(0\leq n\leq N-1\)。
虽然圆周运算是源自于对周期信号的处理,但是经过一般化的扩展之后,对有限长序列也可以进行圆周运算。具体就是,你可以把有限长序列以它的长度为周期,进行周期延拓成一个周期序列,然后进行运算,然后取其主值区间进行观察得到的结果。
圆周反褶就是一个周期序列进行反褶之后,取其主值区间序列。因为一个周期序列反褶之后还是周期序列,所以这么做是合理的。
假设一周期信号在其主值区间的取值为\[x[n]=\{x[0],x[1],x[2],x[3],x[4]\}\]即该序列的周期为\(5\),那么反褶后的信号为(只关注主值区间)
\[
\begin{aligned}
y[0]&=x[0]=x[0] \y[1]&=x[-1]=x[5-1]=x[4] \y[2]&=x[-2]=x[5-2]=x[3] \y[3]&=x[-3]=x[5-3]=x[2] \y[4]&=x[-4]=x[5-4]=x[1]
\end{aligned}
\]
为了方便用数学的语言描述这种运算,首先看一种数学上的模运算运算,首先看几个模运算的例子:
\[
\begin{aligned}
2 \,mod \, 5 =2 \6 \, mod \, 5 = 1 \-3 \, mod \, 5 = 2
\end{aligned}
\]
不知道大家看出来没有,模运算其实就是求余,\(2\)对\(5\)的余数就是\(2\),\(6\)对于\(5\)的余数是\(1\),而\(-3\)对\(5\)的余数应该为\((-3+5)\, mod\, 5=2\)(加上\(5\)之后不影响余数的大小,因为\(5\)一直能整除\(5\),\(5\)对\(5\)的余数一直是\(0\))
我们把\(2 \, mod\, 5\)记作\(<2>_5\),所以我们定义圆周反褶为
\[y[n]=x[<-n>_N]\]
其中\(N\)为序列\(x[n]\)的长度。
由上面的公式可以看出,与一般的反褶不同的是,序列下标经过了一次模运算。并且经过上面的数学化的定以后,圆周运算就不仅仅只对周期信号有效了,对一般的有限长信号都是有效的。
用计算画图看一下进行圆周反褶后的效果:
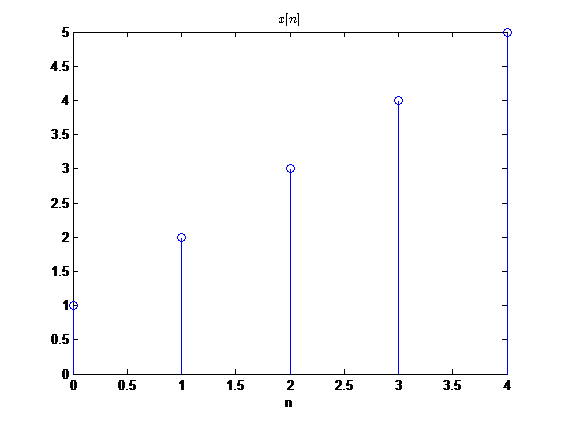
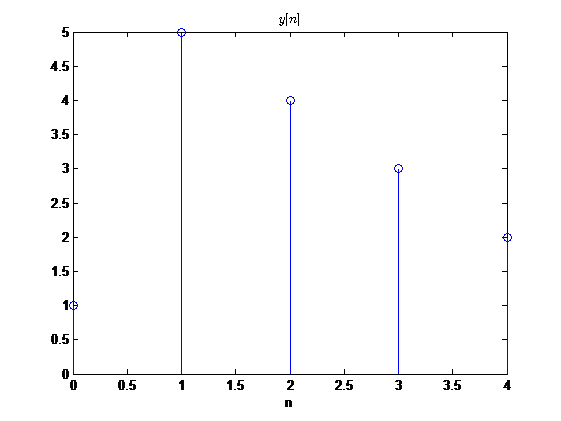
而一般的反褶又是什么样子的呢?还是通过计算机画图观察:

看到这里二者发现不仅波形不一样,并且有值区间也不一样,一般反褶的有值区间变为了\(-4 \leq n \leq 0\),而圆周反褶的有值区间是\(0 \leq n \leq 4\)。
这个例子给出的就是有限长序列的圆周反褶运算,圆周运算是从周期序列扩展而来的,但不仅仅只针对于周期序列。事实上,后面的处理的圆周运算大部分都是有限长的序列。
由圆周反褶的概念,不难定义出圆周时移,即:
\[y[n]=x[<n-n_0>_N]\]
与圆周反褶类似,\(y[n]\)的有值区间还是与\(x[n]\)相同。
我们来直观的感受一下,圆周时移到底是怎么一个效果:
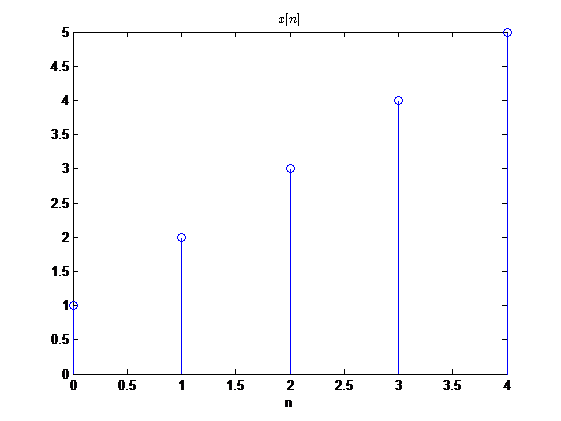
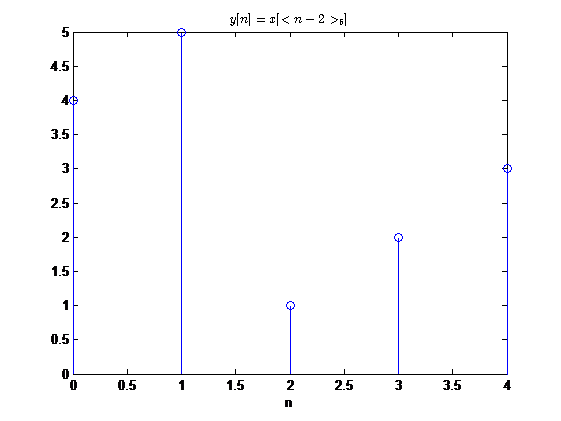
这完全可以看做是将序列进行周期延拓之后,然后进行时移,取其主值区间进行观察得到的结果。
设两周期信号\(\tilde{x}[n],\tilde{w}[n]\)的周期都为\(N\),它们的线性卷积为
\[
\tilde{y}[n]=\sum_{m=-\infty}^{\infty}\tilde{x}[m]\tilde{w}[n-m]
\]
易知序列\(\tilde{y}[n]\)也为周期序列,其周期为\(N\)。
设序列\(\tilde{y}[n]\)的主值区间为\(y[n]\),\(\tilde{y}[n]\)的\(DFS\)为\(\tilde{Y}[k]\),\(y[n]\)的\(DFT\)为\(Y[k]\),由\(DFS\)与\(DFT\)的关系,得到\(Y[k]\)为\(\tilde{Y}[k]\)的主值区间。
\[
\tilde{Y}[k]=\tilde{X}[k]\tilde{W}[k]
\]
\(\tilde{X}[k]\)为序列\(\tilde{x}[n]\)的\(DFS\),\(\tilde{W}[k]\)为序列\(\tilde{w}[n]\)的\(DFS\),所以得到
\[
Y[k]=X[k]W[k], \, 0 \leq k \leq N-1
\]
则
\[
\begin{aligned}
y[n]&=\frac{1}{N}\sum_{k=0}^{N-1}Y[k]e^{j\frac{2\pi kn}{N}} \&=\frac{1}{N}\sum_{k=0}^{N-1}X[k]W[k]e^{j\frac{2\pi kn}{N}} \&=\frac{1}{N}\sum_{k=0}^{N-1}\sum_{m=0}^{N-1}x[m]e^{-j\frac{2\pi km}{N}}W[k]e^{j\frac{2\pi kn}{N}} \&=\sum_{m=0}^{N-1}x[m](\frac{1}{N}\sum_{k=0}^{N-1}W[k]e^{j\frac{2\pi k(n-m)}{N}}) \&=\sum_{m=0}^{N-1}x[m]w[<n-m>_N]
\end{aligned}
\]
所以定义有限长序列的圆周卷积为
\[
\color{red}y[n]=\sum_{m=0}^{N-1}x[m]w[<n-m>_N]=x[n]\text{\textcircled N}w[n]
\]
其中序列\(x[n]\)和序列\(w[n]\)的长度都为\(N\),易知卷积后的序列\(y[n]\)的长度也为\(N\)。
考虑两有限长序列\(x[n]?\)和\(w[n]?\),\(x[n]?\)的有值区间为\(0\backsim N_1-1?\),即其长度为\(N_1?\),\(w[n]?\)的有值区间为\(0\backsim N_2-1?\),其长度为\(N_2?\),记其线性卷积为\(y[n]?\),则
\[
y[n]=\sum_{m=-\infty}^{\infty}x[m]w[n-m]=\sum_{m=0}^{N_1-1}x[m]w[n-m]?
\]
其长度为\(M=N_1+N_2-1?\)
为了求其圆周卷积\(y_{L}[n]\),将\(x[n]\)和\(w[n]\)补零延拓为长度为\(L\)的序列,其中\(L\geq max\{N_1,N_2\}\),则
\[
\begin{aligned}
y_L[n]&=\sum_{m=0}^{L-1}x[m]w[<n-m>_L], \, 0 \leq n \leq L-1\&=\sum_{m=0}^{L-1}x[m]\tilde{w}[n-m], \, 0 \leq n \leq L-1 \&=\sum_{m=0}^{L-1}x[m]\sum_{k=-\infty}^{\infty}w[n-m-kL], \, 0 \leq n \leq L-1 \&=\sum_{k=-\infty}^{\infty}\sum_{m=0}^{L-1}x[m]w[n-kL-m], \, 0 \leq n \leq L-1 \&=\sum_{k=-\infty}^{\infty}y[n-kL], \, 0 \leq n \leq L-1
\end{aligned}
\]
所以L点圆周卷积是其线性卷积以周期为L进行周期延拓得到的结果。

由上图(这里不好画离散的图,用连续的表示一下,原理是一样的)知,当\(L>N_1+N_2-2=M-1\)时,即\(L\geq M\)时,即序列补零扩展后的长度大于线性卷积后的长度时
\[
\sum_{k=-\infty}^{\infty}y[n-kL]
\]
未发生混叠,取其主区间即是圆周卷积\(y_L[n]\),取圆周卷积\(y_L[n]\)的前\(N_1+N_2-1\)个点就是线性卷积\(y[n]\)的值。
但是当\(L < M\)时
\[
\sum_{k=-\infty}^{\infty}y[n-kL]
\]
发生了混叠,如下图
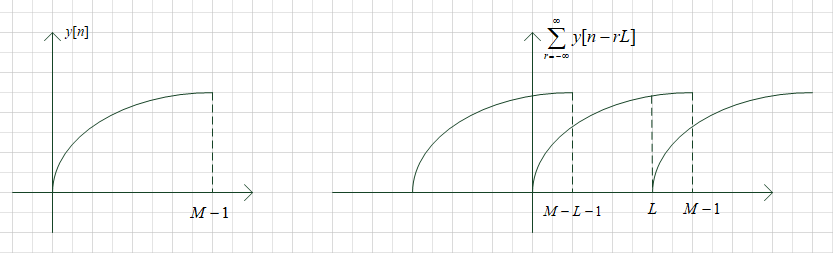
由图可知,只有\(M-L \backsim L-1\)这\(2L-M\)个点未发生混叠。所以如果补零扩展得到的长度\(L<M\)的话,那么得到圆周卷积\(y_L[n]\)中,只有在\(M-L \backsim L-1\)的取值与线性卷积的取值相同。
所以用圆周卷积计算有限长序列线性卷积的方法为:
原文:https://www.cnblogs.com/LastKnight/p/10958044.html