参考[http://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/]
计算diffuse irradiance map或者求解sh系数的时候,需要对整个球面进行积分,由于cubemap不同位置的像素投影到球面上面积不同,所以不能平等的对待所有像素。
这时候就需要计算每个像素对应的solid angle。
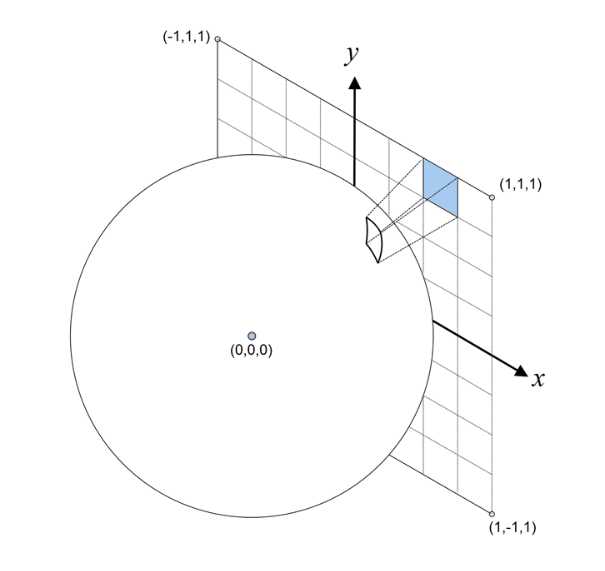
如图,单位球位于原点。选取cubemap的一个面,假设其位于z=1的平面上。一个像素的立体角大小就是其投影到球面上的面积。
关于面积的求解分三步进行:
1. 计算平面上一点(x,y,1)投影到球面上后的坐标p‘。
2. p‘关于x方向和y方向的方向导数,两个方向导数叉乘的模长即为微面元的面积。
3. 对微面元积分,求得(0,0,1)- (x,y,1)对应四边形的投影面积(立体角),然后利用这个公式就能求得一个像素的立体角。
-----------------------------------------------------------------------------------------------------------------------
1. p‘就是一个放缩操作:
![]()
2. 两个方向导数:
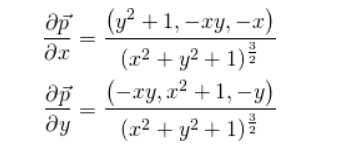
这两个向量叉乘的结果:

然后叉乘的模长即为微面元的面积:
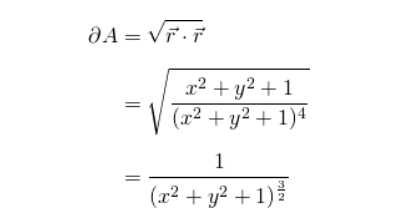
3. 积分,计算(0,0)到像素点(s,t)的立体角
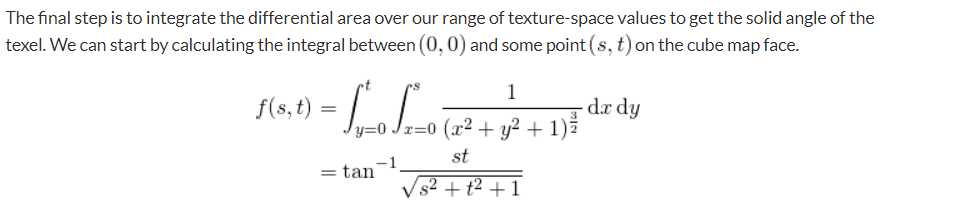
4. 如果想计算四边形ABCD的立体角,则:S = f(A) - f(B) + f(C) - f(D)
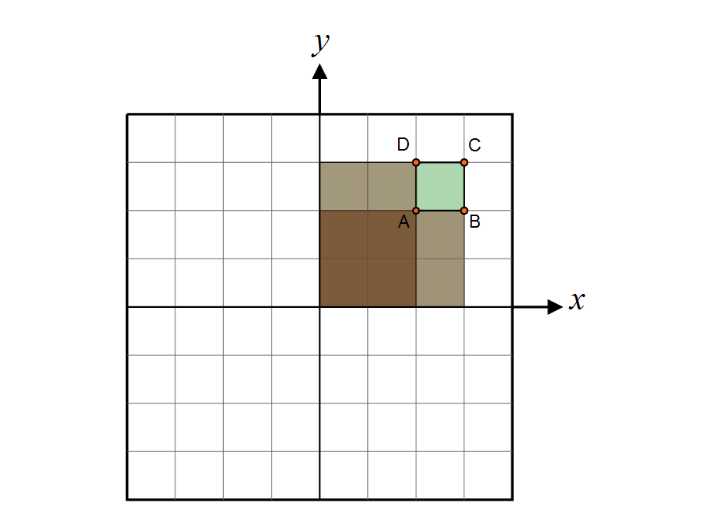
--------------------------------------------------------------------------------------------------------------------------------------------
代码:
double sphereQuadrantArea(double x, double y) {
return std::atan2(x*y, std::sqrt(x*x + y*y + 1));
}
double solidAngle(size_t dim, size_t u, size_t v) {
const double iDim = 1.0f / dim;
double s = ((u + 0.5) * 2*iDim) - 1;
double t = ((v + 0.5) * 2*iDim) - 1;
const double x0 = s - iDim;
const double y0 = t - iDim;
const double x1 = s + iDim;
const double y1 = t + iDim;
double solidAngle = sphereQuadrantArea(x0, y0) -
sphereQuadrantArea(x0, y1) -
sphereQuadrantArea(x1, y0) +
sphereQuadrantArea(x1, y1);
return solidAngle;
}
Solid Angle of A Cubemap Texel - 计算Cubemap的一个像素对应的立体角的大小
原文:https://www.cnblogs.com/redips-l/p/10976173.html