这里的内容参考了:
- 邱锡鹏老师的《神经网络与深度学习》
- 吴恩达老师的《深度学习》课程
由于所有的样本数据都被用来训练模型,验证模型时,也只是将模型的训练结果与正确结果作对比来观察正确率。这样的训练方法是否正确?正确率能否作为评价模型的标准?该如何正确评价一个模型?以及采取何种改进策略?
当模型表现不佳时?通常出现两种问题,一种是高偏差问题,另一种是高方差问题。
偏差: 是指一个模型的在不同训练集上的平均性能和最优模型的差异,可以用来衡量一个模型的拟合能力。
方差: 是指一个模型在不同训练集上的差异,可以用来衡量一个模型是否容易过拟合。
以下图中给出了机器学习算法的偏差和方差的四种不同组合情况。每个图的中心点为最优模型f?(x),蓝点为不同训练集D上得到的模型 fD(x) 。
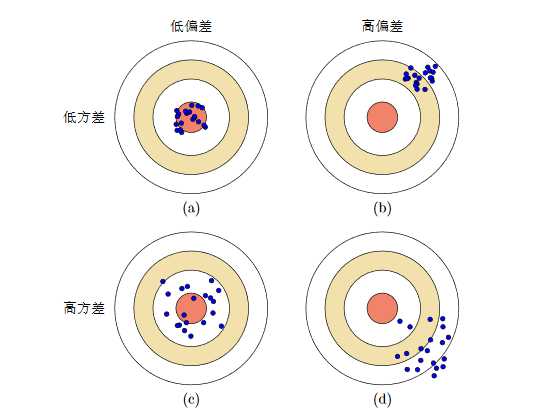
上图所示为偏差和方差的四种组合:
(a)低方差-低偏差:理想情况;
(b)低方差-高偏差:模型泛化能力很好,但拟合能力不足;
(c)高方差-低偏差:模型拟合能力很好,但泛化能力较差;
(d)高方差-高偏差:最差情况。
就像打靶一样,偏差描述了射击总体是否偏离目标,而方差描述射击准不准。
方差一般会随着训练样本的增加而减少。当样本足够多时,方差比较少,可以选择能力强的模型来减少偏差。然而在很多机器学习任务上,训练集往往比较有限,最优的偏差和最优的方差就无法兼顾。
随着模型复杂度的增加,模型的拟合能力增强,偏差减小而方差增大,从而导致过拟合。以结构错误最小化为例,可以通过调整正则化系数r来控制模型的复杂度。当r增大时,模型复杂度降低,方差减小而偏差上升,从而避免过拟合。但当r过大时,总的期望错误反而会上升。因此,一个好的正则化系数需要在偏差和方差之间取得较好的平衡。如下图所示,最优模型并不一定是偏差曲线和方差曲线的交点。

原文:https://www.cnblogs.com/xxxxxxxxx/p/10975281.html