接着压位OvO。。。
我不会告诉你答案就是卡特兰数。。。
为什么呢?
首先,$ans[0]=1,ans[1]=1,ans[2]=2$
对于$ans[3]$,我们可以发现他是这样来的:
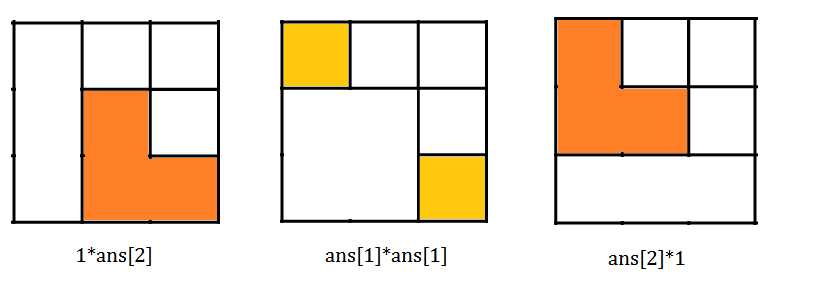
$ans[3]=\sum_{i=0}^{3-1}ans[i]*ans[n-i-1]$
而$ans[4]$呢?
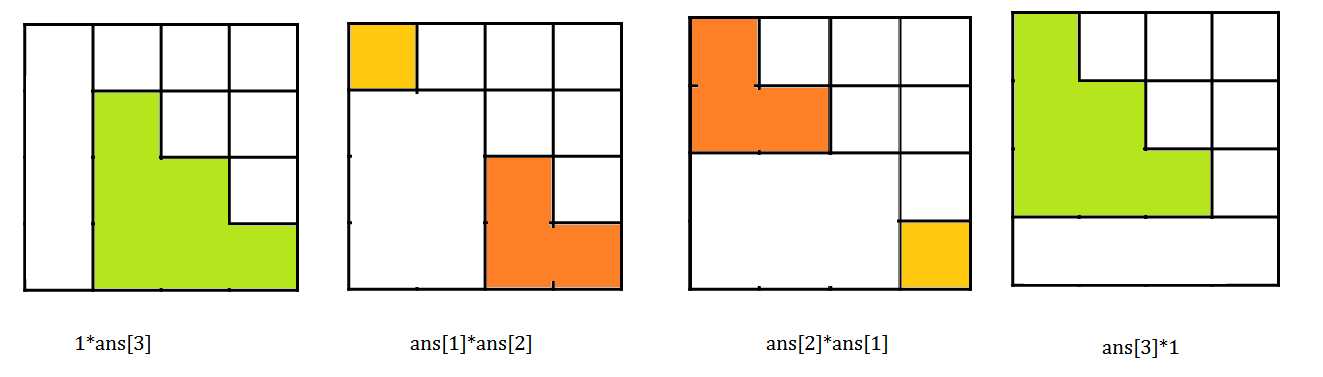
$ans[4]=\sum_{i=0}^{4-1}ans[i]*ans[n-i-1]$
woc。。。这不是卡特兰数嘛。。。
最后:要用高精qwq
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<cmath> #include<cctype> #include<cstdlib> #include<vector> #include<map> #include<set> #define ll long long #define R register ll static char RD[1<<15],*S=RD,*D=RD; #define getchar() (S==D&&(D=(S=RD)+fread(RD,1,1<<15,stdin),S==D)?EOF:*S++) const int W=9,B=1E+9,N=1010,L=1000; using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch==‘-‘?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } struct Int { int sz; ll dat[2010]; Int() {sz=0; memset(dat,0,sizeof(dat));} inline void init(int vl) { sz=0; while(vl) ++sz,dat[sz]=vl%B,vl/=B; } inline void print() { printf("%lld",dat[sz]); for(R i=sz-1;i;--i) printf("%09d",dat[i]); } }; Int operator *(Int a,int b) { Int c; R lst=a.sz; for(R i=1;i<=lst;++i) c.dat[i]=a.dat[i]*b; for(R i=1;i<=lst;++i) c.dat[i+1]+=c.dat[i]/B,c.dat[i]%=B; while(c.dat[lst+1]) ++lst,c.dat[lst+1]+=c.dat[lst]/B,c.dat[lst]%=B; c.sz=lst; return c; } Int ans; int c[N],n; inline void add(int x,int v) { for(R i=2;i*i<=x;++i) while(x%i==0) x/=i,c[i]+=v; if(x!=1) c[x]+=v; } signed main() { #ifdef JACK freopen("NOIPAK++.in","r",stdin); #endif n=g(); for(R i=n+2;i<=2*n;++i) add(i,1); for(R i=1;i<=n;++i) add(i,-1); ans.dat[1]=ans.sz=1; for(R i=1;i<=2*n;++i) while(c[i]) ans=ans*i,--c[i]; ans.print(); }
2019.06.05

Luogu P2532 [AHOI2012]树屋阶梯 卡特兰数
原文:https://www.cnblogs.com/Jackpei/p/10977070.html