题目

Given an array nums of n integers, are three elements a, b, c in nums such that a+b+c=0? Find all unique triplets in the array which gives the sum of zero.
Note：
The solution set must not contain duplicate triplets.
Example：
> Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[[-1, 0, 1],[-1, -1, 2]]

思路

双指针法变种——三指针法（这里的指针指的是数组下标）

• 要保证三个数a+b+c=0；
  • 至少要保证有一个数是0或者负数，
  • 但是由于数组是乱序排列的，很难直接判断是否有0或负数，于是想到将数组排序
• 将等式改写为b+c = -a，如何找到
  • 首先保证a是非正数（0或负数）
  • 如何找到b和c使之与-a相等？
    • 定义中间指针p2、尾指针p3,移动的方向为往中间移动
      
• 不能有重复结果
  • 在最外层循环时，跳过已经判断过的数字
  • p2、p3往中间移动时，跳过重复元素

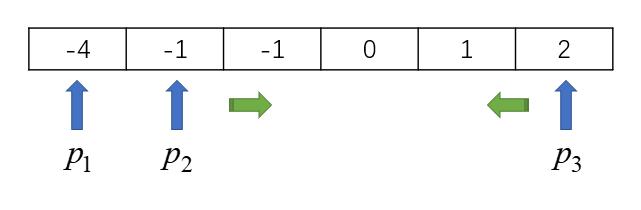
于是
Step1：将数组排序
Step2：以第一个数p1作为最外层循环，其中如果第一个数如果为正，说明和不可能为0
Step3：定义中间指针p2，尾指针p3，

• 如果num[p2] + num[p3] > -nums[p1]，则说明和太小了，应该往数值大的方向的移动，p2++
• 如果num[p2] + num[p3] < -nums[p1]，则说明和太大了，应该往数值小的方向的移动，p3--
• 如果num[p2] + num[p3] = -nums[p1]，将结果保存，同时将p2、p3往中间移动，为了保证结果的唯一性，需要跳过重复元素

C++

vector<vector<int>> threeSum(vector<int>& nums) {

  vector<vector<int> > resVec;
  sort(nums.begin(),nums.end());  //将nums从小到大排序

  for(int p1=0;p1<nums.size();p1++){
    if(nums[p1] >0)  //如果第一个数为正数，说明肯定不存在三个数
      return resVec;
    if(p1>0 && nums[p1] == nums[p1-1])  //由于结果需要唯一性，故去除nums中的重复元素
      continue;
    int p2 = p1+1;//中间指针
    int p3 = nums.size()-1;//尾指针
    while(p2<p3){
      int a = nums[p1];//非正
      int b = nums[p2];
      int c = nums[p3];
      if(b+c== -a){
        vector<int> tempVec(3);
        tempVec[0] = a;
        tempVec[1] = b;
        tempVec[2] = c;
        resVec.push_back(tempVec);
        while (p2 < p3 && nums[p2] == nums[p2 + 1])  //去除重复元素
           p2++;
        while (p2 < p3 && nums[p3 - 1] == nums[p3])  //去除重复元素
           p3--;
        p2++;
        p3--;       
      }
      else if(b+c < -a){   //如果b+c之和小于-a，说明和太小了，应该往数值大的方向的移动
        p2++;
      }
      else{  //反之，如果b+c之和大于-a，说明和太大了，应该往数值小的方向的移动
        p3--;
      }
    }       
  }
  return resVec;
}

Python

15. 3Sum[M]三数之和

原文：https://www.cnblogs.com/Jessey-Ge/p/10993487.html