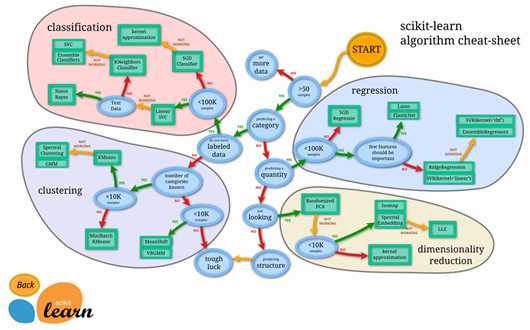
scikit-learn主要由分类、回归、聚类和降维四大部分组成,其中分类和回归属于有监督学习范畴,聚类属于无监督学习范畴,降维适用于有监督学习和无监督学习。scikit-learn的结构示意图如下所示:
 scikit-learn中的聚类算法主要有:
scikit-learn中的聚类算法主要有:
K 均值聚类(K-Means Clustering)是最基础和最经典的基于划分的聚类算法,是十大经典数据挖掘算法之一。它的基本思想是,通过迭代方式寻找K个簇的一种划分方案,使得聚类结果对应的代价函数最小。特别地,代价函数可以定义为各个样本距离所属簇中心点的误差平方和(SSE)。
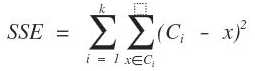
迭代停止条件:

1 print(__doc__) 2 3 # Author: Phil Roth <mr.phil.roth@gmail.com> 4 # License: BSD 3 clause 5 6 import numpy as np 7 import matplotlib.pyplot as plt 8 9 from sklearn.cluster import KMeans 10 from sklearn.datasets import make_blobs 11 12 plt.figure(figsize=(12, 12)) 13 14 n_samples = 1500 15 random_state = 170 16 X, y = make_blobs(n_samples=n_samples, random_state=random_state) 17 18 # Incorrect number of clusters 19 y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X) 20 21 plt.subplot(221) 22 plt.scatter(X[:, 0], X[:, 1], c=y_pred) 23 plt.title("Incorrect Number of Blobs") 24 25 # Anisotropicly distributed data 26 transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]] 27 X_aniso = np.dot(X, transformation) 28 y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso) 29 30 plt.subplot(222) 31 plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred) 32 plt.title("Anisotropicly Distributed Blobs") 33 34 # Different variance 35 X_varied, y_varied = make_blobs(n_samples=n_samples, 36 cluster_std=[1.0, 2.5, 0.5], 37 random_state=random_state) 38 y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied) 39 40 plt.subplot(223) 41 plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred) 42 plt.title("Unequal Variance") 43 44 # Unevenly sized blobs 45 X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])) 46 y_pred = KMeans(n_clusters=3, 47 random_state=random_state).fit_predict(X_filtered) 48 49 plt.subplot(224) 50 plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred) 51 plt.title("Unevenly Sized Blobs") 52 53 plt.show()
原文:https://www.cnblogs.com/xc-family/p/11006525.html