
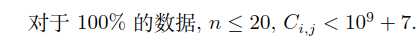
考场不要降智。
不一定是连续的一段放在一块,。。。
容斥。f[s]=g[s]-∑f[t]*g[s-t]
t必须包含1
子集卷积
注意,子集卷积过程与s包含1无关,最后再清空即可。

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^‘0‘) #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch==‘-‘)&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+‘0‘);} template<class T>il void ot(T x){if(x<0) putchar(‘-‘),x=-x;output(x);putchar(‘ ‘);} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar(‘\n‘);} namespace Modulo{ const int mod=1e9+7; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } using namespace Modulo; namespace Miracle{ const int N=21; int n; int c[N][N]; int g[N][1<<N]; int h[1<<N]; int f[N][1<<N]; int sz[1<<N]; int lg[1<<N]; void FWT(int *f,int n,int c){ for(reg p=2;p<=n;p<<=1){ for(reg l=0;l<n;l+=p){ for(reg k=l;k<l+p/2;++k){ if(c==1){ inc(f[k+p/2],f[k]); }else{ f[k+p/2]=ad(f[k+p/2],mod-f[k]); } } } } } int main(){ rd(n); for(reg i=0;i<n-1;++i){ for(reg j=1;j<=n-i-1;++j){ rd(c[i][i+j]);c[i+j][i]=c[i][i+j]; } } for(reg i=0;i<n;++i) lg[1<<i]=i; for(reg s=0;s<(1<<n);++s){ sz[s]=sz[s>>1]+(s&1); } g[0][0]=1; for(reg s=1;s<(1<<n);++s){ int now=lg[s&(-s)]; g[sz[s]][s]=g[sz[s]-1][s-(s&(-s))]; for(reg j=0;j<n;++j){ if(j!=now&&((s>>j)&1)){ g[sz[s]][s]=mul(g[sz[s]][s],ad(1,c[now][j])); } } } // for(reg i=0;i<=n;++i){ // // for(reg s=0;s<(1<<n);++s){ // // cout<<g[i][s]<<" "; // // }cout<<endl; // // } f[0][0]=1; f[1][1]=1; FWT(f[0],(1<<n),1); FWT(f[1],(1<<n),1); FWT(g[0],(1<<n),1); FWT(g[1],(1<<n),1); // prt(g[1],0,(1<<n)-1); // prt(f[1],0,(1<<n)-1); for(reg i=2;i<=n;++i){ // memset(ff,0,sizeof ff); // memset(gg,0,sizeof gg); // cout<<" ii------------ "<<i<<endl; for(reg t=1;t<i;++t){ for(reg s=1;s<(1<<n);++s){ // if((s&1)&&(__builtin_popcount(s)==i)){ f[i][s]=ad(f[i][s],mul(f[t][s],g[i-t][s])); // } } } // prt(f[i],0,(1<<n)-1); FWT(f[i],(1<<n),-1); // prt(f[i],0,(1<<n)-1); for(reg s=0;s<(1<<n);++s){ if((s&1)&&(__builtin_popcount(s)==i)){ f[i][s]=sub(g[i][s],f[i][s]); }else f[i][s]=0; } // prt(f[i],0,(1<<n)-1); FWT(g[i],(1<<n),1); if(i!=n) FWT(f[i],(1<<n),1); } cout<<f[n][(1<<n)-1]; return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */

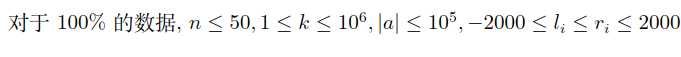
咕

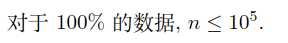
最大的连通块抠出子树放到最小连通块里。
分最大连通块是某个子树,和往父亲走两种情况。
后者可以前序遍历后序遍历建立两棵主席树。
原文:https://www.cnblogs.com/Miracevin/p/11027870.html