线段树是修改，查找一组数据比较常用的数据类型，相对树状数组来说，线段树更加灵活，可以完美实现单点和区间的查找与修改，甚至可以做到树状数组做不到的区间赋值修改。

线段树及存值方式

　　线段树不同于树状数组，线段树是一棵真正的树，它具有左子树和右子树，每一个节点存有一个初始序列一个区间内区间和，且两个子节点所存的区间和之和等于父节点所存的区间和，假设每一个节点的信息如下图所示：

l~r代表此节点存有初始序列区间l~r的区间和；sum即为区间l~r的区间和；k代表节点序号

一个线段树就如下图所示：

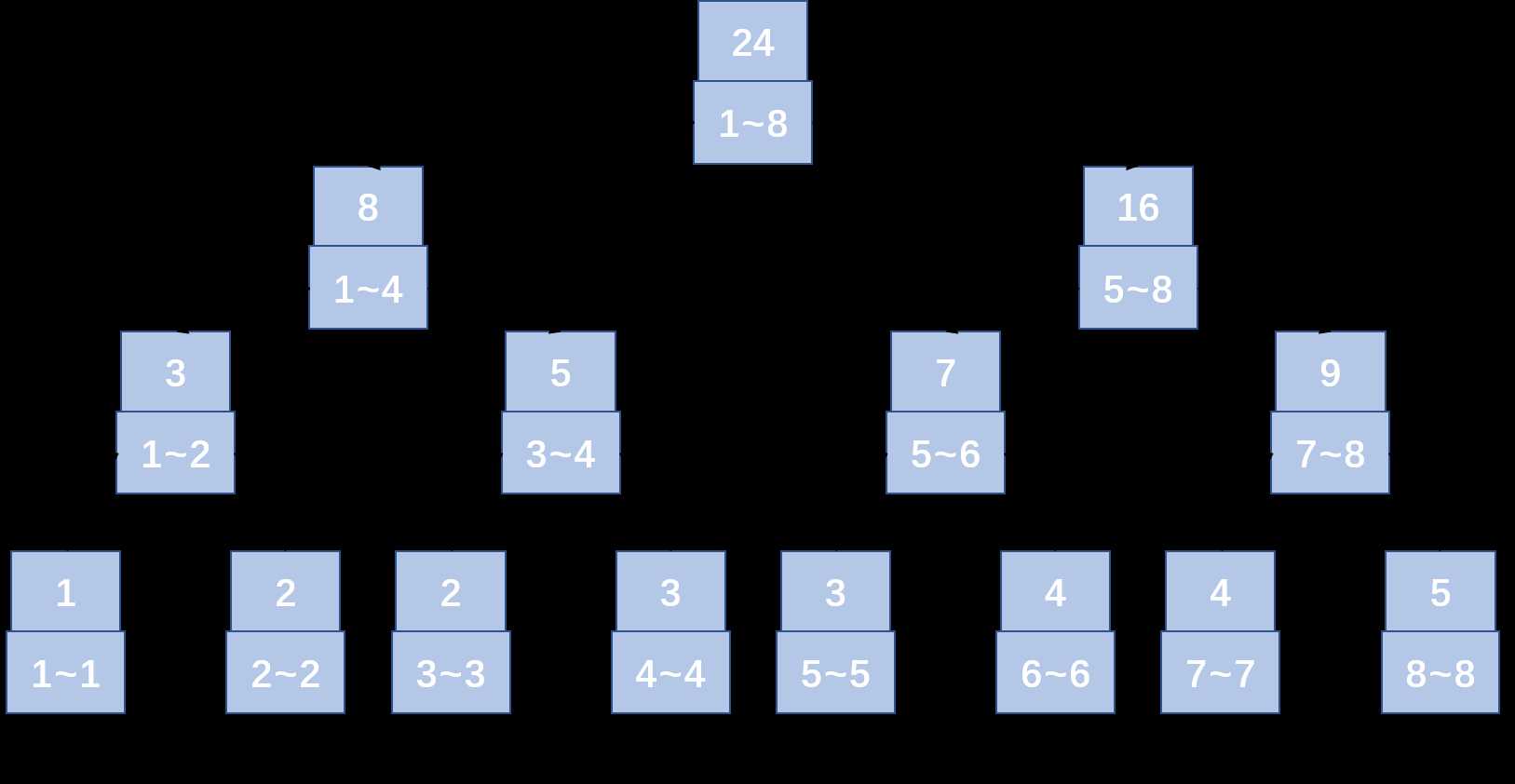
可以发现：一个节点的序号如果是k，那么左子节点的序号为2*k，右子节点的序号为2*k+1，由于这种对应关系，所以线段树在建树过程中不需要重新定义指针指向子节点。

父节点的区间为两个子节点的区间和：假设两个子节点存有初始序列l₁~r₁及l₂~r₂（r₁<l₂）的区间和，那么对应父节点存有l₁~r₂的区间和，叶子节点则只存有初始序列每一个点的值。

ps：注意用结构体数组存节点信息时，如果初始序列区间长为n，那么结构体数组要开4*n的空间！

证明：

　　假设区间长为n，那么线段树最下面一次至多有n个节点，则这棵树有⌈log₂n⌉+1层，由于 ⌈log₂n⌉小于等于log₂n+1。所以这棵树至多有log₂n+2层，根据二叉树的节点个数与层数的关系可知，这棵树至多有2^log₂n+2=4*n个节点。

 博客还没写完，，学习仍在继续。。。

学习：数据结构----线段树

原文：https://www.cnblogs.com/qiyueliu/p/11032134.html