树上差分建立在差分数组的基础上,所以还不会差分数组的大佬可以先预习一下这篇博客,期望阅读时间5分钟:差分数组。
引入这样一个例题,给定一棵n(n≤105)个点的树,m(m≤105)次操作,将这棵树上的两点之间的最短路径上的每一个点都加k或者都减k,在这m次操作之后求出每个点的值。
首先,在你没有学过树上差分的时候,你会想到用tarjan或者是倍增求出这两个点的LCA然后暴力更改,显然这样每一次操作时间复杂度最劣会是O(n),显然不能接受。
那么我们现在引入树上差分。
树上差分我们可以先感性的理解为树上的差分数组。
树上差分分为两种,一种是边的差分,另一种是点的差分。
那么今天我们就先来讲一下点的差分。
大家现在一定会想像差分数组从前往后扫一样从根往下扫,每个点存它与它的父亲的差,但是认真想一下,这样会存在一个问题,如果我将一条路径上每个点的值都增加k,那么这条路径上的其它枝杈都要打标记减去k。
如图:
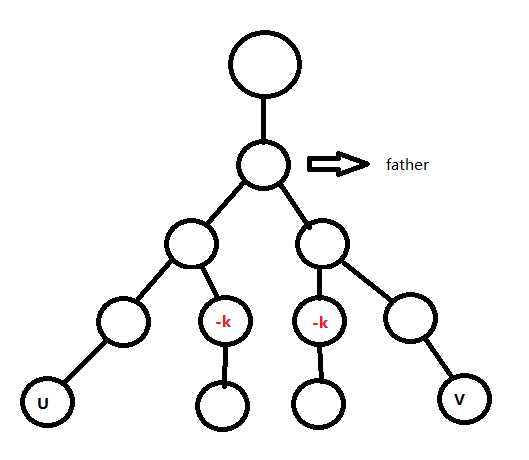
这样当路径上的枝杈过多时,时间复杂度会非常不优。
(未完,持续更新中……)
原文:https://www.cnblogs.com/wzc521/p/11032383.html