三角剖分的种类很多, 根据不同需求有各种各样的算法, 这里讲的是按顺序给出边缘顶点之后, 如何对这个顶点集合进行三角剖分.
比如下面的图示:
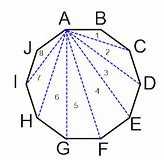 图一
图一
给出了边缘点并按顺序排列, 将它剖分成三角形, 虽然有多种方法, 不过我们只需要获得正确的三角形就行了, 不用关心它剖成怎么样.
对于凸多边形(Convex Polygon), 只需要像图中一样, 找一个起始点, 然后按顺序取点跟起始点组成三角形就行了, 非常简单. 代码都懒得写了.
而对于凹多边形(Concave Polygon)就不能简单划分三角形了, 因为会超出原有多边形的范围 :
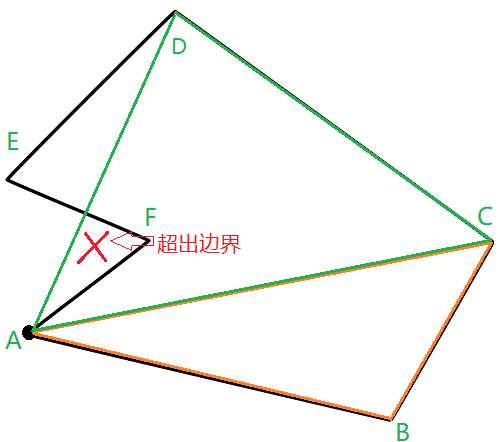 图二
图二
ACD组成的三角形明显超出了边界, 不能简单剖分.
PS: 不要把这个和 delaunay triangulation 搞混了, delaunay做的是离散点的三角剖分, 获得的是这些离散点组成的凸多边形.
我是最近才有这个功能要做, 所以找了一下相关的实现方法, 发现很多人的实现基于很早以前的某篇论文<<三维模型重建中的凹多边形三角剖分>> : 解放军测绘学院学报 1999年9月刊.
而且看了下基本都是抄来抄去, 代码不少, 错误不少, 基本都没有实现这个剖分逻辑...... 论文也是很有问题, 给出了几个定义, 几个性质, 然后就给出了算法, 至于算法的正确性证明也没有, 我就
直接相信它吧.
把论文的算法精简出来就有那么几步 ( 比如顶点列表为 List<Vector3> points, 排列顺序就是在List中的顺序 ) :
一. 寻找出一个凸顶点
1.1 定义: 临时从列表中去掉某个顶点, 然后列表剩下的顶点构成新的的多边形, 这个被去掉的顶点不在新多边形内部, 就是凸顶点 ( 比如图二中的 A, B, C, D, E 点都是凸顶点, F点被AE组成的多边形包在里面, 所以不是凸顶点 )
1.2 功能 : 如果不是凸顶点, 把这个顶点插回列表原来位置. 找下一个顶点, 如果是凸顶点, 测试是否可划分顶点.
二. 确定该凸顶点是可划分顶点
2.1 定义 : 被去除掉的点和原列表中左右相邻的点组成的三角形, 如果不包含列表中的其它顶点, 就是可划分点 ( 比如图二中的 ABC 里面没有其它点, B点就是可划分点. ACD 中有F点C点就不可划分 )
2.2 功能 : 如果不是可划分顶点, 把这个顶点插回列表原来位置. 找下一个顶点
三. 可划分就把顶点从列表中删除
3.1 功能 : 把之前该点组成的三角形记录到返回值列表中, 它就是一个剖分出来的三角形. 不插回去就等于删除了.
四. 一直重复直到只剩最后3个顶点, 最后3个顶点就是最后一个三角形.
4.1 功能 : 把最后三个顶点作为一个三角形加到返回值列表中, 剖分就完成了.
说明一下我用的是Unity3D, 原始顶点列表作为输入, 返回值输出的是剖分后的三角形顶点, 而不是组成三角形的Index, 因为Mesh需要normal的数量跟顶点数量一致, 如果Mesh使用原始顶点列表作为顶点的话(比如正方体只有8个顶点),
然后通过Mesh.triangles 来设置三角形的话, 它自动计算出来的normal也是只有8个, 也就是说它把各个共享顶点的向量进行了插值, 光照会出错的.
下来就是代码实现了
原文:https://www.cnblogs.com/tiancaiwrk/p/11052699.html