深度学习-笔记 第2章 线性代数 2.6特殊类型的矩阵和向量

2.6 特殊类型的矩阵和向量

对角矩阵：只在主对角线上含有非零元素，其他位置都是零。形式上，矩阵D是对角矩阵，当且仅当对于所有的i ≠ j, D_{i, j} = 0。

单位矩阵：是对角矩阵，其对角元素全部是1。

用diag(v)表示对角元素由向量v中元素给定的一个对角方阵。

如图：

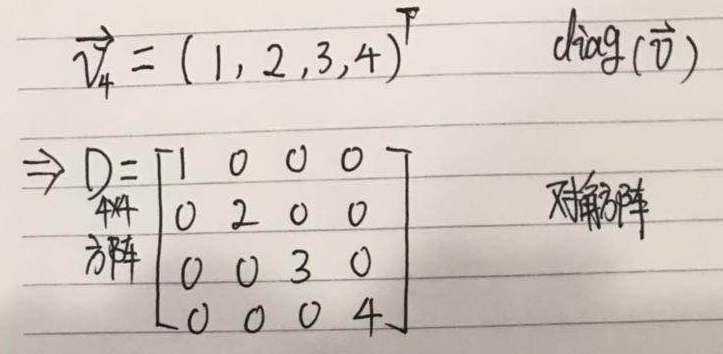
对角方阵的逆矩阵：diag(v)^{-1 =} diag([1/v₁,...,1/v_n])

计算乘法diag(v)x，我们只需要将x中的每个元素x_i放大v_i倍。换言之，diag(v)x = v圈点x

并非所有的对角矩阵都是方阵。长方形的矩阵也有可能是对角矩阵。非方阵的对角矩阵没有逆矩阵。

对于长方形对角矩阵D而言，乘法Dx会涉及x中每个元素的缩放，如果D是瘦长型矩阵，那么在缩放后的末尾添加一些零；如果D是胖宽型矩阵，那么在缩放后去掉最后一些元素。

如图：

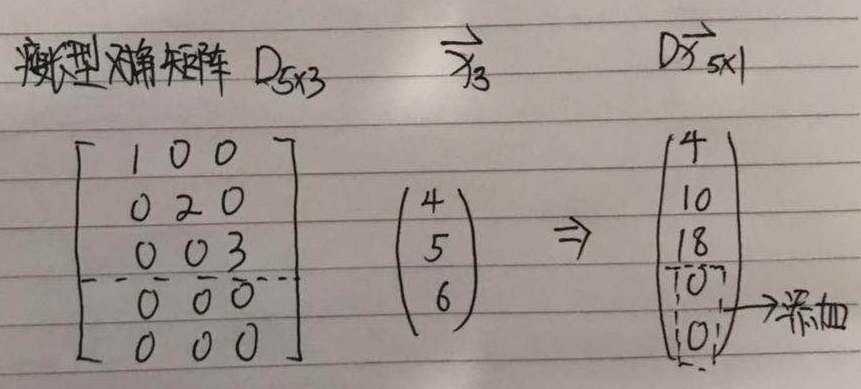
对阵矩阵：是转置和自己相等的矩阵，即A = A^T

单位向量：是具有单位范数的向量，即||x||₂ = 1

正交：如果x^Ty = 0，那么向量x和向量y互相正交

标准正交：如果有n个（范数非零）向量不但互相正交，而且范数都为1，那么我们称他们是标准正交。

正交矩阵：指行向量和列向量是分别标准的正交方阵，即A^TA = AA^T = I => A^-1 = A^T

深度学习-笔记 第2章 线性代数 2.6特殊类型的矩阵和向量

原文：https://www.cnblogs.com/luciusCheung/p/11063112.html