大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
菲波那切数列是最经典的用来做递归举例的案例,但是用菲波那切数列的复杂度为2的指数次方,时间复杂度非常高,当n很大时还会造成栈溢出
分析求解过程
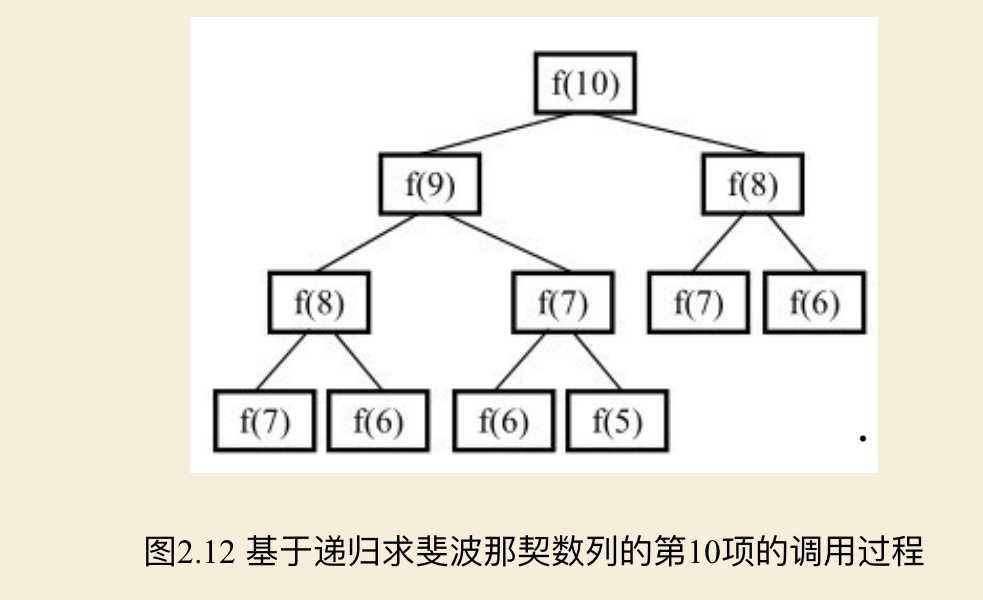
可以看到很多节点的值被重复计算了,因此我们可以采用自下而上用循环的方式保存上一次计算的值避免重复计算,由f(0)、f(1)计算出f(2),由f(1)、f(2)计算出f(3)
由此类推,则时间复杂度为O(n)
1 public int Fibonacci(int n) { 2 if(n==0 ||n==1) 3 return n; 4 else{ 5 return Fibonacci(n-1)+Fibonacci(n-2); 6 } 7 }
1 public int Fibonacci(int n) { 2 if(n==0){ 3 return 0; 4 } 5 int fibMinusOne = 1,fibMinusTwo = 0; 6 for(int i=1;i<n;i++){ 7 int tmp = fibMinusOne; 8 fibMinusOne = fibMinusOne + fibMinusTwo; 9 fibMinusTwo = tmp; 10 } 11 return fibMinusOne; 12 }
原文:https://www.cnblogs.com/huanglf714/p/11069624.html