巨佬制作人们大家好,我是练习多项式两周半的个人练习生lgl。这里总结一下多项式基本操作。
1.多项式加、减、输出
不说了。
时间复杂度$O(n)$。
2.多项式取模
已知多项式$F(x)$,求它对$x^n$取模。
人话:把$n$次及以上的系数清零。
时间复杂度$O(n)$。
3.多项式乘法/卷积
(1)$FFT$
依靠复平面上瞎转以及强大的$double$。

#include<cmath> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define N 2000050 #define ll long long const double Pi = acos(-1.0); template<typename T> inline void read(T&x) { T f=1,c=0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=10*c+ch-‘0‘;ch=getchar();} x = f*c; } struct cp { double x,y; cp(){} cp(double x,double y):x(x),y(y){} cp operator + (const cp&a)const{return cp(x+a.x,y+a.y);} cp operator - (const cp&a)const{return cp(x-a.x,y-a.y);} cp operator * (const cp&a)const{return cp(x*a.x-y*a.y,x*a.y+y*a.x);} }; int n,m,mx,to[2*N],lim=1,L; void fft(cp *a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { cp w0(cos(Pi/i),k*sin(Pi/i)); for(int j=0;j<len;j+=(i<<1)) { cp w(1,0); for(int o=0;o<i;o++,w=w*w0) { cp w1 = a[j+o],w2 = a[j+o+i]*w; a[j+o] = w1+w2; a[j+o+i] = w1-w2; } } } } cp a[2*N],b[2*N],c[2*N]; int main() { read(n),read(m);mx = max(n,m); for(int i=0;i<=n;i++)read(a[i].x); for(int i=0;i<=m;i++)read(b[i].x); while(lim<=2*mx)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); fft(a,lim,1),fft(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]; fft(c,lim,-1); for(int i=0;i<=n+m;i++) printf("%lld ",(ll)(c[i].x/lim+0.5)); puts(""); return 0; }
注意那个重载运算符,写在里面是可以连加连乘的。
(2)$NTT$
需要一个好模数,还要依靠原根的优秀性质。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define N 2000050 #define ll long long #define MOD 998244353 template<typename T> inline void read(T&x) { T f=1,c=0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=10*c+ch-‘0‘;ch=getchar();} x = f*c; } ll fastpow(ll x,int y) { ll ret = 1; while(y) { if(y&1)ret=ret*x%MOD; x=x*x%MOD;y>>=1; } return ret; } int n,m,mx,to[2*N],lim=1,l; void ntt(ll *a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { ll w0 = fastpow(3,(MOD-1)/(i<<1)); for(int j=0;j<len;j+=(i<<1)) { ll w = 1; for(int o=0;o<i;o++,w=w*w0%MOD) { ll w1 = a[j+o],w2 = a[j+o+i]*w%MOD; a[j+o] = (w1+w2)%MOD; a[j+o+i] = ((w1-w2)%MOD+MOD)%MOD; } } } if(k==-1) for(int i=1;i<(lim>>1);i++)swap(c[i],c[lim-i]); } ll a[2*N],b[2*N],c[2*N]; int main() { read(n),read(m);mx = max(n,m); for(int i=0;i<=n;i++)read(a[i]); for(int i=0;i<=m;i++)read(b[i]); while(lim<=2*mx)lim<<=1,l++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(l-1))); ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); ll inv = fastpow(lim,MOD-2); for(int i=0;i<lim;i++)c[i]=c[i]*inv%MOD; for(int i=0;i<=n+m;i++)printf("%lld ",c[i]); puts(""); return 0; }
自测不开$O2$时$NTT$较快,开了$O2$之后$FFT$更快。
(3)任意模数$NTT$
我的版本是用$FFT$+$long\;double$把系数拆成$x/M$和$x\;mod\;M$,之后再合并。

#include<cmath> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define double long double typedef long long ll; const int N = 500050; const double Pi = acos(-1.0); template<typename T> inline void read(T&x) { T f = 1,c = 0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=c*10+ch-‘0‘;ch=getchar();} x = f*c; } int n,m,MOD; struct cp { double x,y; cp(){} cp(double x,double y):x(x),y(y){} cp operator + (const cp&a)const{return cp(x+a.x,y+a.y);} cp operator - (const cp&a)const{return cp(x-a.x,y-a.y);} cp operator * (const cp&a)const{return cp(x*a.x-y*a.y,x*a.y+y*a.x);} }; int to[N],lim,L; void init() { lim = 1,L = 0; while(lim<=2*max(n,m))lim<<=1,L++; for(int i=1;i<lim;i++) to[i] = ((to[i>>1]>>1)|((i&1)<<(L-1))); } ll A[N],B[N],C[N]; void fft(cp*a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { cp w0(cos(Pi/i),k*sin(Pi/i)); for(int j=0;j<len;j+=(i<<1)) { cp w(1,0); for(int o=0;o<i;o++,w=w*w0) { cp w1 = a[j+o],w2 = a[j+o+i]*w; a[j+o] = w1+w2; a[j+o+i] = w1-w2; } } } if(k==-1) for(int i=0;i<len;i++)a[i].x/=len; } cp a[N],b[N],c[N],d[N],e[N],f[N],g[N],h[N]; void mtt() { int M = 32768; for(int i=0;i<max(n,m);i++) { a[i].x = A[i]/M,b[i].x = A[i]%M; c[i].x = B[i]/M,d[i].x = B[i]%M; } fft(a,lim,1),fft(b,lim,1),fft(c,lim,1),fft(d,lim,1); for(int i=0;i<lim;i++) { e[i] = a[i]*c[i],f[i] = a[i]*d[i]; g[i] = b[i]*c[i],h[i] = b[i]*d[i]; } fft(e,lim,-1),fft(f,lim,-1),fft(g,lim,-1),fft(h,lim,-1); for(int i=0;i<lim;i++) C[i] = (((ll)(e[i].x+0.1))%MOD*M%MOD*M%MOD+((ll)(f[i].x+0.1))%MOD*M%MOD +((ll)(g[i].x+0.1))%MOD*M%MOD+((ll)(h[i].x+0.1))%MOD)%MOD; } int main() { read(n),read(m),read(MOD);n++,m++; init(); for(int i=0;i<n;i++)read(A[i]); for(int i=0;i<m;i++)read(B[i]); mtt(); for(int i=0;i<n+m-1;i++)printf("%lld ",C[i]); puts(""); return 0; }
时间复杂度$O(nlogn)$。大常数。
(4)更强的$MTT$
参见myy论文。

void mtt(int*F,int*G,int*H,int len) { get_lim(len<<1); for(register int i=0;i<lim;++i)a[i]=b[i]=cp(0,0); for(register int i=0;i<len;++i) a[i]=cp(F[i]&(M-1),F[i]>>15),b[i]=cp(G[i]&(M-1),G[i]>>15); fft(a,lim,1),fft(b,lim,1); for(register int i=0;i<lim;++i) { int j = (lim-i)&(lim-1); c[j]=cp(0.5*(a[i].x+a[j].x),0.5*(a[i].y-a[j].y))*b[i]; d[j]=cp(0.5*(a[i].y+a[j].y),0.5*(a[j].x-a[i].x))*b[i]; } fft(c,lim,1),fft(d,lim,1); for(register int i=0;i<lim;++i) { int kaa = (ll)(c[i].x/lim+0.5)%MOD; int kab = (ll)(c[i].y/lim+0.5)%MOD; int kba = (ll)(d[i].x/lim+0.5)%MOD; int kbb = (ll)(d[i].y/lim+0.5)%MOD; Mod(H[i] = ((ll)kaa+((ll)(kab+kba)<<15)%MOD+((ll)kbb<<30)%MOD)%MOD+MOD); } }
4.多项式求导、积分
不会求导积分建议出门左转高中数学教材。

void down(ll*a,int len) { for(int i=0;i+1<len;i++) a[i]=a[i+1]*(i+1)%MOD; a[len-1]=0; } void up(ll*a,int len) { for(int i=len-1;i>0;i--) a[i]=a[i-1]*inv(i)%MOD; a[0] = 0; }
求导时间复杂度$O(n)$,积分$O(n)$或者$O(nlog)$。
5.多项式求逆
已知多项式$F(x)$,求$G(x)$满足$$F(x)*G(x)≡1\;(mod\;x^n)$$
一个多项式对应的逆是一个唯一的无穷极的多项式,我们要求的是它的前$n$项。
一般都是倍增法求解。
我们现在知道$$F(x)*G0(x)≡1\;(mod\;x^{\frac{n}{2}})$$
移项:$$F(x)*G0(x)-1≡0\;(mod\;x^{\frac{n}{2}})$$
搞模的次数,整体平方:$$(F(x)*G0(x)-1)^2≡0\;(mod\;x^n)$$
打开:$$F^2*G0^2-2*F*G0+1≡0\;(mod\;x^n)$$
两边乘上$G$,得$$F*G0^2-2*G0+G≡0\;(mod\;x^n)$$
再移项:$$G≡2*G0-F*G0^2$$
这个式子减号左边是$\frac{n}{2}$次的,减号右边是$n$次的。
注意右边乘的话先$G*G$再乘$F$,注意长度。

void get_inv(int len,int*F,int*G) { if(len==1){G[0]=fastpow(F[0],MOD-2);return ;} get_inv(len>>1,F,G),mtt(G,G,T,len>>1),mtt(T,F,H,len); for(register int i=0;i<len;++i)Mod(G[i]=G[i]*2%MOD-H[i]+MOD); }
边界条件$G_0= \frac{1}{F_0}$,时间复杂度$O(nlogn)$。
6.多项式整除、取余
给出$F(x),G(x)$,其中$F(x)$是$n$次的,$G(x)$是$m$次的。
求$$F(x)=Q(x)*G(x)+R(x)$$
$R(x)$次数$m-1$,$Q(x)$次数$n-m$。
神奇变换:$$F(\frac{1}{x})=Q(\frac{1}{x})*G(\frac{1}{x})+R(\frac{1}{x})$$
然后同乘$x^n$,发现$$F(\frac{1}{x})*x^n=Q(\frac{1}{x})*x^{n-m}*G(\frac{1}{x})*x^{m}+R(\frac{1}{x})*x^n$$
$$F_R(x)=Q_R(x)*G_R(x)+R_R(x)$$
其中$F_R(x)$表示将$F$系数反转得到的多项式,$Q_R(x)$、$G_R(x)$同理。
但是我们发现$R(x)$是$m-1$次的,乘完之后后面会有一堆0。所以$$F_R(x)≡Q_R(x)*G_R(x)\;(mod\;x^{n-m})$$
反过来求逆就好了。
把$Q(x)$求出来之后求$R(x)$就是多项式乘法、多项式减法。
时间复杂度$O(nlogn)$。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; const int N = 600050; const int MOD = 998244353; template<typename T> inline void read(T&x) { T f = 1,c = 0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=c*10+ch-‘0‘;ch=getchar();} x = f*c; } ll fastpow(ll x,int y) { ll ret = 1; while(y) { if(y&1)ret=ret*x%MOD; x=x*x%MOD;y>>=1; } return ret; } int n,m,to[N],lim,L; void ntt(ll*a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { ll w0 = fastpow(3,(MOD-1)/(i<<1)); for(int j=0;j<len;j+=(i<<1)) { ll w = 1; for(int o=0;o<i;o++,w=w*w0%MOD) { ll w1 = a[j+o],w2 = a[j+o+i]*w%MOD; a[j+o] = (w1+w2)%MOD; a[j+o+i] = (w1-w2+MOD)%MOD; } } } if(k==-1) { for(int i=1;i<len>>1;i++)swap(a[i],a[len-i]); ll inv = fastpow(len,MOD-2); for(int i=0;i<len;i++)a[i]=a[i]*inv%MOD; } } ll f[N],g[N],a[N],b[N],c[N]; void sol(int len) { if(len==1) { g[0] = fastpow(f[0],MOD-2); return ; } int mid = (len+1)>>1; sol(mid); lim = 1,L = 0; while(lim<=2*len)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=f[i]; for(int i=0;i<mid;i++)b[i]=g[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)g[i]=(2*g[i]%MOD-c[i]+MOD)%MOD; } void mul(ll*A,ll*B,int len) { lim = 1,L = 0; while(lim<=2*len)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=A[i],b[i]=B[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); } ll F[N],G[N],H[N],R[N],F0[N],G0[N]; int main() { read(n),read(m),n++,m++; for(int i=0;i<n;i++)read(F[i]); for(int i=0;i<m;i++)read(G[i]); memcpy(F0,F,sizeof(F0)); memcpy(G0,G,sizeof(G0)); reverse(F,F+n);reverse(G,G+m); for(int i=0;i<m;i++)f[i]=G[i]; sol(n-m+1);mul(F,g,n-m+1); for(int i=0;i<n-m+1;i++)H[i]=c[i]; reverse(H,H+n-m+1); mul(H,G0,n); for(int i=0;i<n-m+1;i++)printf("%lld ",H[i]); puts(""); for(int i=0;i<m-1;i++)printf("%lld ",(F0[i]-c[i]+MOD)%MOD); puts(""); return 0; }
7.多项式开根
这个黑科技是小朋友与二叉树之后大佬们搞出来的。
已知$F(x)$,求$G(x)$满足$$G(x)*G(x)≡F(x)\;(mod\;x^n)$$
和多项式的逆一样,一个多项式的根是惟一的。
依然考虑倍增求解。
假设我们已知$$H(x)*H(x)≡F(x)\;(mod\;x^{\frac{n}{2}})$$,要求$G(x)$。
常规移项平方:$$(H^2(x)-F(x))^2≡0\;(mod\;x^n)$$
然后是一个神奇操作:$$(H^2(x)+F(x))^2≡4F(x)H^2(x)\;(mod\;x^n)$$
然后再移项:$$\frac{(H^2(x)+F(x))^2}{4H^2(x)} ≡ F(x) \; (mod\;x^n)$$
然后惊奇的发现左边是平方形式,所以$$G(x) ≡ \frac{H^2(x)+F(x)}{2H(x)} \; (mod\;x^n)$$
递归的时候套一个多项式求逆即可(反正才四行),注意清数组不然可能会死。
时间复杂度$T(n)=T(n/2)+O(nlogn)=O(nlogn)$,大常数。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; const int N = 600050; const int MOD = 998244353; template<typename T> inline void read(T&x) { T f = 1,c = 0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=c*10+ch-‘0‘;ch=getchar();} x = f*c; } ll fastpow(ll x,int y) { ll ret = 1; while(y) { if(y&1)ret=ret*x%MOD; x=x*x%MOD;y>>=1; } return ret; } int to[N],lim,L; void ntt(ll*a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { ll w0 = fastpow(3,(MOD-1)/(i<<1)); for(int j=0;j<len;j+=(i<<1)) { ll w = 1; for(int o=0;o<i;o++,w=w*w0%MOD) { ll w1 = a[j+o],w2 = a[j+o+i]*w%MOD; a[j+o] = (w1+w2)%MOD; a[j+o+i] = (w1-w2+MOD)%MOD; } } } if(k==-1) { for(int i=1;i<len>>1;i++)swap(a[i],a[len-i]); ll inv = fastpow(len,MOD-2); for(int i=0;i<len;i++)a[i]=a[i]*inv%MOD; } } int n; ll a[N],b[N],c[N]; void get_lim(int len) { lim = 1,L = 0; while(lim<=len)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); } void mul(ll*A,int Alen,ll*B,int Blen) { get_lim(Alen+Blen); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<Alen;i++)a[i]=A[i]; for(int i=0;i<Blen;i++)b[i]=B[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); } ll F[N],G[N],H[N]; void get_inv(int len) { if(len==1) { H[0] = fastpow(G[0],MOD-2); return ; } int mid = (len+1)>>1; get_inv(mid); get_lim(len<<1); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=G[i]; for(int i=0;i<mid;i++)b[i]=H[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)H[i]=(2*H[i]%MOD-c[i]+MOD)%MOD; } void get_sqrt(int len) { if(len==1) { G[0] = 1; return ; } int mid = (len+1)>>1; get_sqrt(mid); for(int i=0;i<len;i++)H[i]=0; get_inv(len); mul(G,mid,G,mid); for(int i=0;i<len;i++)G[i]=(c[i]+F[i])%MOD; mul(G,len,H,len); for(int i=0;i<len;i++)G[i]=c[i]*((MOD+1)/2)%MOD; } int main() { read(n); for(int i=0;i<n;i++)read(F[i]); get_sqrt(n); for(int i=0;i<n;i++)printf("%lld ",G[i]); puts(""); return 0; }
8.多项式对数函数(ln)
已知$F(x)$,求$$G(x)≡ln(F(x))\;(mod\;x^n)$$
直接求导即可:$$G‘(x)≡F‘(x)*\frac{1}{F(x)}$$
所以说求导求逆积分即可。
时间复杂度$O(nlogn)$。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; const int N = 600050; const int MOD = 998244353; template<typename T> inline void read(T&x) { T f = 1,c = 0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=c*10+ch-‘0‘;ch=getchar();} x = f*c; } ll fastpow(ll x,int y) { ll ret = 1; while(y) { if(y&1)ret=ret*x%MOD; x=x*x%MOD;y>>=1; } return ret; } ll inv(ll x){return fastpow(x,MOD-2);} int to[N],lim,L; void down(ll*a,int len) { for(int i=0;i+1<len;i++) a[i]=a[i+1]*(i+1)%MOD; a[len-1]=0; } void up(ll*a,int len) { for(int i=len-1;i>0;i--) a[i]=a[i-1]*inv(i)%MOD; a[0] = 0; } void ntt(ll*a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { ll w0 = fastpow(3,(MOD-1)/(i<<1)); for(int j=0;j<len;j+=(i<<1)) { ll w = 1; for(int o=0;o<i;o++,w=w*w0%MOD) { ll w1 = a[j+o],w2 = a[j+o+i]*w%MOD; a[j+o] = (w1+w2)%MOD; a[j+o+i] = (w1-w2+MOD)%MOD; } } } if(k==-1) { for(int i=1;i<len>>1;i++)swap(a[i],a[len-i]); ll inv = fastpow(len,MOD-2); for(int i=0;i<len;i++)a[i]=a[i]*inv%MOD; } } int n; ll a[N],b[N],c[N]; ll F[N],G[N]; void get_inv(int len) { if(len==1) { G[0] = inv(F[0]); return ; } int mid = (len+1)>>1; get_inv(mid); lim = 1,L = 0; while(lim<2*len)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=F[i]; for(int i=0;i<mid;i++)b[i]=G[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)G[i]=(2*G[i]%MOD-c[i]+MOD)%MOD; } int main() { read(n); for(int i=0;i<n;i++)read(F[i]); get_inv(n);down(F,n); lim = 1,L = 0; while(lim<=2*n)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1]>>1)|((i&1)<<(L-1))); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<n;i++)a[i]=F[i]; for(int i=0;i<n;i++)b[i]=G[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<n;i++)F[i]=c[i]; up(F,n); for(int i=0;i<n;i++)printf("%lld ",F[i]); puts(""); return 0; }
9.多项式指数函数(exp)
已知$F(x)$,求$$G(x)≡e^{F(x)}\;(mod\;x^n)$$
附加牛顿迭代:$x=x‘-\frac{f(x‘)}{f(x‘)‘}$
牛迭原理?一张图:
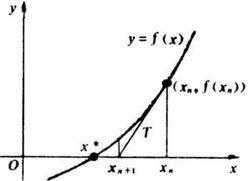
回到问题,依然倍增求解,假设已知$$H(x)≡e^{F(x)}\;(mod\;x^{\frac{n}{2}})$$
先对式子取ln再移项:$$ln(H(x))-F(x)≡0\;(mod\;x^{\frac{n}{2}})$$
然后呢……
我们把它当做$ln(x)-k=0$,问题转化为式子求零点,那么把牛迭套进去有这样一个式子:$$G(x)≡H(x)-\frac{ln(H(x))-F(x)}{\frac{1}{H(x)}}\;(mod\;x^n)$$
分数太难看了,变一下:$$G(x)≡H(x)*(1-ln(H(x))+F(x))\;(mod\;x^n)$$
左转把多项式ln板子带过来即可。
复杂度?$T(n)=T(n/2)+O(nlogn)=O(nlogn)$?
常数?卡死人。
我的$ntt$跑$1e6$的数据:
我的$exp$跑$1e5$的数据:

卡常好啊

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef unsigned long long ll; const int N = 600050; const int MOD = 998244353; template<typename T> inline void read(T&x) { T f = 1,c = 0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){c=c*10+ch-‘0‘;ch=getchar();} x = f*c; } ll fastpow(ll x,int y) { ll ret = 1; while(y) { if(y&1)ret=ret*x%MOD; x=x*x%MOD;y>>=1; } return ret; } int to[N],lim,L; ll W[N],Inv; void Mod(ll&x){if(x>=MOD)x-=MOD;} void ntt(ll*a,int len,int k) { for(int i=0;i<len;i++) if(i<to[i])swap(a[i],a[to[i]]); for(int i=1;i<len;i<<=1) { ll w0 = W[i]; for(int j=0;j<len;j+=(i<<1)) { ll w = 1; for(int o=0;o<i;o++,w=w*w0%MOD) { ll w1 = a[j+o],w2 = a[j+o+i]*w%MOD; Mod(a[j+o] = w1+w2); Mod(a[j+o+i] = w1-w2+MOD); } } } if(k==-1) { for(int i=1;i<len>>1;i++)swap(a[i],a[len-i]); for(int i=0;i<len;i++)a[i]=a[i]*Inv%MOD; } } ll a[N],b[N],c[N]; void get_lim(int len) { lim = 1,L = 0; while(lim<=len)lim<<=1,L++; for(int i=1;i<lim;i++)to[i]=((to[i>>1])>>1|((i&1)<<(L-1))); for(int i=1;i<lim;i<<=1)W[i]=fastpow(3,(MOD-1)/(i<<1)); Inv = fastpow(lim,MOD-2); } int n; ll A[N],F[N],G[N],H[N];//F,lnF,1/G void get_inv(int len) { if(len==1) { H[0] = fastpow(G[0],MOD-2); return ; } int mid = (len+1)>>1; get_inv(mid);get_lim(len<<1); for(int i=0;i<=lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=G[i]; for(int i=0;i<mid;i++)b[i]=H[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)Mod(H[i]=2*H[i]%MOD-c[i]+MOD); } void down(ll*a,int len) { for(int i=0;i<len;i++)a[i]=a[i+1]*(i+1)%MOD; a[len-1]=0; } void up(ll*a,int len) { for(int i=len-1;i;i--)a[i]=a[i-1]*fastpow(i,MOD-2)%MOD; a[0] = 0; } void get_ln(int len) { for(int i=0;i<len;i++)G[i]=F[i],H[i]=0; get_inv(len);down(G,len); get_lim(len<<1); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=G[i],b[i]=H[i]; ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)G[i]=c[i]; up(G,len); } void get_exp(int len) { if(len==1) { F[0] = 1; return ; } int mid = (len+1)>>1; get_exp(mid); for(int i=0;i<len;i++)G[i]=0; get_ln(len); get_lim(len<<1); for(int i=0;i<lim;i++)a[i]=b[i]=0; for(int i=0;i<len;i++)a[i]=F[i],b[i]=(A[i]-G[i]+MOD)%MOD; Mod(++b[0]); ntt(a,lim,1),ntt(b,lim,1); for(int i=0;i<lim;i++)c[i]=a[i]*b[i]%MOD; ntt(c,lim,-1); for(int i=0;i<len;i++)F[i]=c[i]; } int main() { read(n); for(int i=0;i<n;i++)read(A[i]); get_exp(n); for(int i=0;i<n;i++)printf("%llu ",F[i]); puts(""); return 0; }
大概就这些了吧。
(是时候总结一下常用卡常技巧了)
原文:https://www.cnblogs.com/LiGuanlin1124/p/11024466.html