特征选择能够提升模型的性能,更能帮助我们理解数据的特点、底层结构,改善模型算法增强模型繁华能力,减少过拟合。特征提取的方法分为3种:Filter过滤法、Wrapper包裹式、Embedded嵌入法
1.过滤法
移除低方差特征(不需要特征值):计算各个特征的方差,设定阈值,选择方差>阈值的特征
以波士顿房价预测数据集和鸢尾花数据集为例
from sklearn.datasets import load_boston
boston = load_boston()
from sklearn.datasets import load_iris
iris = load_iris()#导入IRIS数据集
len(boston.data[0])#13个特征
1 a1=fs.VarianceThreshold(threshold=1).fit_transform(boston.data) 2 len(a1[0]) 3 10 4 from sklearn.linear_model import LinearRegression 5 def c5(x): 6 s1=LinearRegression(fit_intercept=True) 7 s1.fit(x,boston.target) 8 return s1.score(x,boston.target)#给出此模型的可决系数,可决系数越大越好 9 print(c5(a1)) 10 0.7246070392219914 11 #不同阈值下的方差特征选择,并拟合求对应的可决系数 12 for i in np.arange(0.,1,0.1): 13 a1=fs.VarianceThreshold(threshold=i).fit_transform(boston.data) 14 print(c5(a1),len(a1[0]),i) 15 #特征的选择应用场景:减少训练时间时,需强调模型的可解释性时 16 #首先特征数量较多时,易出现过拟合,特征选择可防止过拟合
与目标值对比进行筛选
#SelectkBest:选择评分最高的k个特征
#SelectPercentile:保留最高得分百分比之几的特征
#自带对比函数
#对于分裂:chi2,f_classif,mutual_info_classif
#对于回归:f_regression,mutual_info_regression
#chi2用于分类问题,衡量自变量对因变量的相关性
#F-test:f_classif/f_regression的方法计算两个随机变量之间的线性相关程度
1 #卡方检验chi2 2 a1=fs.SelectKBest(fs.chi2,k=3).fit_transform(iris.data,iris.target)#选择卡房值前三的特征 3 a1.shape 4 a2=fs.SelectPercentile(fs.chi2,percentile=40).fit_transform(iris.data,iris.target) 5 a2.shape#选择卡方检验前40%的特征
1 #f_test 2 b1=np.array([2,3,12]) 3 b2=np.array([2,3,10]) 4 b3=b1[:,np.newaxis] 5 print(fs.f_regression(b3,b2))#分别对应f-value和p-value
1 a3=fs.SelectPercentile(fs.f_regression,percentile=40).fit_transform(boston.data,boston.target) 2 a3#选择排名前40%的特征,对波士顿放假预测数据集回归 3 a4=fs.SelectKBest(fs.f_regression,k=4).fit_transform(boston.data,boston.target) 4 a4#选择排名前4的特征
1 互信息:计算任何种类的统计相关性 2 a5=fs.SelectKBest(fs.mutual_info_regression,k=3).fit_transform(boston.data,boston.target) 3 a5 4 array([[ 2.31 , 6.575, 4.98 ], 5 [ 7.07 , 6.421, 9.14 ], 6 [ 7.07 , 7.185, 4.03 ], 7 ..., 8 [11.93 , 6.976, 5.64 ], 9 [11.93 , 6.794, 6.48 ], 10 [11.93 , 6.03 , 7.88 ]])
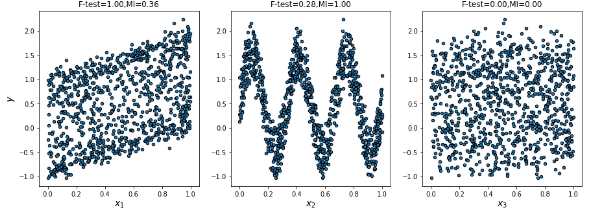
#f检验和互信息的效果比较:y=x1+sin(6*pi*x2)+0.1*rand(0,1)
1 from sklearn.feature_selection import f_regression,mutual_info_regression 2 np.random.seed(0)#设置随机数种子 3 x=np.random.rand(1000,3)#产生向量(x1,x2,x3) 4 y=x[:,0]+np.sin(6*np.pi*x[:,1])+0.1*np.random.randn(1000)#计算y值 5 6 f_test,_=f_regression(x,y) 7 f_test/=np.max(f_test)#得到各特征x的f值 8 9 mi=mutual_info_regression(x,y) 10 mi/=np.max(mi)#得到各个特征的互信息的评价指标m1 11 12 plt.figure(figsize=(15,5))#新建画布 13 for i in range(3): 14 plt.subplot(1,3,i+1)#定位在1*3画布的第i个 15 plt.scatter(x[:,i],y,edgecolor=‘black‘,s=20)#做xi和y的散点图 16 plt.xlabel("$x_{}$".format(i+1),fontsize=14)#横坐标 17 if i==0: 18 plt.ylabel("$y$",fontsize=14) 19 plt.title("F-test={:.2f},MI={:.2f}".format(f_test[i],mi[i],fontsize=16)) 20 plt.show()
2.包裹式:用到具体的模型
递归特征消除RFE
:首先,评估器在初始特征集合上训练每一特征并且每一个特征的重要程度用coef和feature_importances获得
#然后移除最不重要的特征,不断迭代重复这个步骤,直到达到所需要的数量为止
#n_features_to_select:为整数时表选出的特征个数,None表选取一半
#step:整数时,每次去除的特征个数,小于1时,为每次去除权重最小的特征
1 from sklearn.linear_model import LinearRegression 2 lr=LinearRegression() 3 rfe=fs.RFE(lr,n_features_to_select=4) 4 s1=rfe.fit(boston.data,boston.target) 5 s1.support_#是否入选的布尔值 6 array([False, False, False, True, True, True, False, False, False, 7 False, True, False, False])
快速特征提取
1 fs.RFE(estimator=LinearRegression(),n_features_to_select=4).fit_transform(boston.data,boston.target)
RFECV
在一个交叉验证的循环中执行的RFE来找到最优的特征数量,对列(特征)进行交叉
#学习器本身不变,最终得到不同特征对于score的重要程度,最后保留最佳的特征组合
#step:整数时,每次取出的特征个数,小于1时每次去除最小权重的特征
#scoring:字符串类型,选择sklearn中的score作为输入对象
#cv:默认为3折,整数为cv数,object:用作交叉验证生成器的对象
#对于迭代器或无输入,若y是二进制或多类,则使用sklearn.model_selection.StratifiedKFold
#若是分类器或y非二进制或多类,则使用sklearn.model_selection.KFold
#StratifiedKFold分层采样交叉切分,确保训练集,测试集中各类别的比例与原始数据集中相同
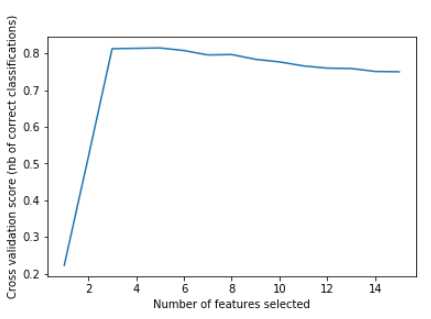
1 from sklearn.svm import SVC 2 from sklearn.model_selection import StratifiedKFold 3 from sklearn.feature_selection import RFECV 4 from sklearn.datasets import make_classification 5 #生成回归模型 6 x,y=make_classification(n_samples=1000,n_features=15,n_informative=3, 7 n_redundant=2,n_repeated=0,n_classes=8, 8 n_clusters_per_class=1,random_state=0) 9 svc=SVC(kernel="linear") 10 rfecv=RFECV(estimator=svc,step=1,cv=StratifiedKFold(2),scoring=‘accuracy‘) 11 rfecv.fit(x,y) 12 print("optimal nu,ber of features:%d"%rfecv.n_features_) 13 14 plt.figure() 15 plt.xlabel("Number of features selected") 16 plt.ylabel("Cross validation score (nb of correct classifications)") 17 plt.plot(range(1,len(rfecv.grid_scores_)+1),rfecv.grid_scores_) 18 plt.show()
3、嵌入法
:SelectFromModel使用具体模型拟合一次,设置阈值,高于阈值的特征值保留
#基于L1的特征选取:使用L1正则化的线性模型会得到稀疏解
1 from sklearn.svm import LinearSVC 2 lsvc=LinearSVC(C=0.01,penalty="l1",dual=False).fit(iris.data,iris.target) 3 model=fs.SelectFromModel(lsvc,prefit=True) 4 xnew=model.transform(iris.data) 5 xnew.shape 6 (150, 3) 7 #Tree的特征选择:在决策树随机森林等训练后,得出不同特征的重要程度,据此进行特征选择 8 from sklearn.ensemble import GradientBoostingClassifier 9 #GBDT作为基模型的特征选择 10 a1=fs.SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data,iris.target) 11 a1.shape 12 (150, 2) 13 rom sklearn.datasets import make_classification 14 from sklearn.ensemble import ExtraTreesClassifier 15 x,y=make_classification(n_samples=1000,n_features=10,n_redundant=0,n_informative=3, 16 n_classes=2,random_state=0,shuffle=False)#定义分类模型 17 forest=ExtraTreesClassifier(n_estimators=250,random_state=0)#随机森林模型实例化 18 forest.fit(x,y)#训练模型 19 importances=forest.feature_importances_#取出模型特征重要性分数 20 std=np.std([tree.feature_importances_ for tree in forest.estimators_],axis=0) 21 indices=np.argsort(importances)[::-1]#特征号 22 for f in range(x.shape[1]): 23 print("%d.feature %d(%f)"%(f+1,indices[f],importances[indices[f]])) 24 model=fs.SelectFromModel(forest,prefit=True) 25 xnew=model.transform(x)#生成新的特征向量 26 xnew.shape 27 (1000, 3)
今天的特征提取没有吃透!要再看,睡觉了
原文:https://www.cnblogs.com/dahongbao/p/11080139.html