在LeetCode上遇到这道题:Add Digits
题目很简单,但是如果要用 O(1) 时间复杂度,不要涉及循环或递归来解答的话,我就不知道如何下手了。
于是我找了一下别人的解法,发现涉及到一个 Digital Root 的原理(由于维基百科打不开,所以我觉得有必要记录一下我搜集到的信息和理解)。
我是从这个网站上看到它的推导过程,但是为了防止以后这些引用的网站不存在或者访问不了,还是得自立更生写一下。
首先,A ≡ B mod C, ≡ 这个符号, 表示 A 和 B mod C 得到的结果一样。(即 同余)
由于一个数的 digital sum 等于它所有位上的数加起来,即:
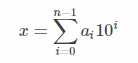
因为 10i ≡1i≡ 1 ( mod 9 ),所以:
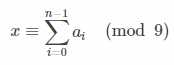
推论出:一个数与它 各个位数和 的模9 同余。
从这个推论我们可以推导出:
f(f(x)) ≡ f(x) ≡ x (mod 9) (x=0 或 9 的情况除外)
为了同时兼顾 x=0 和 x=9 的情况,最后推导出来的公式是:
digital root = 1+ ((x-1) mod 9) (ps: 在计算机计算中,负数的模百家争鸣,所以最好把 0 的计算独立出来,免得为了 -1 % 9 伤脑筋)
1. digital root = 1+ ((x-1) mod 9)
2. 模运算真的能简化大数,好好利用可以省很多事。有空好好研究一下它的其他简化大数的功能。
原文:https://www.cnblogs.com/LinMiaoJia/p/DigitalRoot.html