1.随机森林(RF)
RF是对bagging的进化版,首先都是有放回的进行采样,获得n个训练集从而训练n个弱分类器,但是RF在随机选取的训练集的基础上对于特征的选择也是随机的,随机的选取一部分的特征进行弱分类器的构建,同时在划分建树的过程中也是从这些随机选取的部分特征中选择最优的特征。(使用的为同质个体学习器树模型,对于分类问题的集成策略为投票表决法,对于回归问题的集成策略为平均法)
2.Adaboost
Adaboost是先为训练数据赋予相等的一个权重,然后基于训练数据训练出一个弱分类器,随后计算出该分类器的错误率(错误分类的样本/所有样本的数目),再结合错误率对每个样本的权重进行更新,使得分错的样本其权重变大,同时还会结合错误率为每个分类器赋予不同的权重值。(使用的为同质个体学习器树模型,对于分类问题的集成策略为加权表决法,对于回归问题的集成策略为采用的是对加权的弱学习器取权重中位数对应的弱学习器作为强学习器的方法)
3.GBDT
首先需要明确一点,GBDT中的树都是回归树,为什么?因为该算法由多棵决策树组成,所有树的结论累加起来做最终答案。回归树用于预测实数值,只有实数值其加减才是有意义的,若用分类树,类别的相加毫无意义。
对于建树过程可以参考:https://blog.csdn.net/zpalyq110/article/details/79527653 https://blog.csdn.net/qq_26598445/article/details/80853873
GBDT属于一种加法模型,通过前向分布算法进行求解。
对于回归问题损失函数一般用平方差,它的优点是实现简单便于理解,但是它的缺点也很突出,对于异常值的点会因为平方而得到放大,使得模型的鲁棒性变差。通过建树的过程可以发现,第二棵树是对第一颗树的残差进行拟合,但是这里有一点需要明确,因为案例中所给的损失函数是平方损失函数,因此对它求导之后恰巧和残差的计算方法相同,所以说GBDT并不是说不断的对残差进行拟合,而是对负梯度进行拟合,那里的残差应该是理解为负梯度,上面也分析了平方损失函数的缺点,所以可以把损失函数换成别的损失函数(回归问题常用的还有绝对值损失函数和huber损失函数),一定要明确GBDT是不断对负梯度进行拟合,只是损失函数为平方损失函数时梯度算法恰巧和残差相同,换用其它损失函数负梯度不一定和残差相等,这时候可以称为伪残差。跟普通的梯度下降比,这里的参数是一个模型,梯度也是通过学习到的一个模型,相当于模型的梯度下降。
对于分类问题,GBDT的分类算法从思想上和GBDT的回归算法没有区别,但是由于样本输出不是连续的值,而是离散的类别,导致我们无法直接从输出类别去拟合类别输出的误差。
为了解决这个问题,主要有两个方法,一个是用指数损失函数,此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。
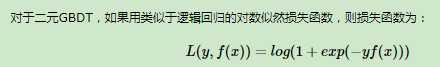
这个损失函数并不是像Logistic回归的损失函数那样是通过极大似然推导出来的,而是设计出来的。
4.XGBoost
对于XGBoost讲解最好的文章:https://blog.csdn.net/qq_22238533/article/details/79477547
通过一步步分析推导来理解
XGBoost为什么用二阶泰勒展开
关于Xgboost用泰勒二阶展开的原因,主要有两点:
1)Xgboost官网上有说,当目标函数是MSE时,展开是一阶项(残差)+二阶项的形式(官网说这是一个nice form),而其他目标函数,如logloss的展开式就没有这样的形式。为了能有个统一的形式,所以采用泰勒展开来得到二阶项,这样就能把MSE推导的那套直接复用到其他自定义损失函数上。简短来说,就是为了统一损失函数求导的形式以支持自定义损失函数。这是从为什么会想到引入泰勒二阶的角度来说的。
2)二阶信息本身就能让梯度收敛更快更准确。这一点在优化算法里的牛顿法里已经证实了。可以简单认为一阶导指引梯度方向,二阶导指引梯度方向如何变化。这是从二阶导本身的性质,也就是为什么要用泰勒二阶展开的角度来说的。
原文:https://www.cnblogs.com/dyl222/p/11093653.html