【例1】递归三角形图案。
输入一个正整数n(n<=7),按图1的示例输出相应的由星号组成的三角形图案。

图1 n分别为2、3、4、5的三角形图案
(1)编程思路。
根据题目示例可知,度数为n的三角形图案,将占2n-1行2n-1列,可以用一个二维字符数组来存储图形中各个字符,因为n<=7,而26=64,因此可以定义一大小为64*64的字符数组来存储度数不超过7的图形。
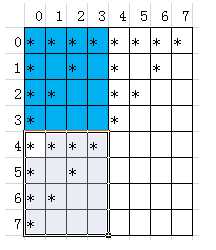
图2
度数n为4的三角形图案在二维数组中的存储情况如图2所示。由图2可知,度数为4的图案可以由度数为3的图案(图2中蓝色底纹所示)复制而来,即在其右方和正下方分别是一个度数为3的图案。
因此,度数为n的图形G(n)可以由以下递归式子表示:
G(n - 1) G(n - 1)
G(n - 1)
设递归函数void draw(int n,int x,int y)表示在(x,y)位置开始设置度数为n的图形,它由3个度数为n-1的图形组成,其起始位置分别为:(x,y)、(x,y+2n-2)和(x+2n-2,y)。
该递归函数的结束条件是:当n=1时(即度数为1的图形),只需在(x,y)位置设置一个字符‘*‘即可。
(2)源程序。
#include <iostream>
using namespace std;
#define N 64
void draw(char a[][N], int n, int row, int col)
{
if(n==1){
a[row][col] = ‘*‘;
return;
}
int w = 1;
int i;
for(i=1; i<=n-2; i++) w *= 2;
draw(a, n-1, row, col);
draw(a, n-1, row, col+w);
draw(a, n-1, row+w,col);
}
int main()
{
char a[N][N];
int n,w,i,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++)
a[i][j] = ‘ ‘;
cin>>n;
w=1;
for(i=1; i<=n-1; i++) w *= 2;
draw(a,n,0,0);
for(i=0; i<w; i++)
{
for(j=0; j<w; j++)
cout<<a[i][j]<<" ";
cout<<endl;
}
return 0;
}
【例2】打印图形(2014年第5届蓝桥杯省赛试题)。
小明在X星球的城堡中发现了如下图形:

编写一个程序,实现该图形的打印。
(1)编程思路。
度数n为4的图案在二维数组中的存储情况如图3所示。由图3可知,度数为4的图案可以由3个度数为3的图案(图3中分别用绿色、浅绿色和黄色蓝色底纹所示)。
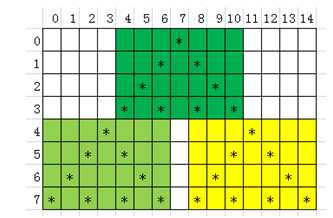
因此,度数为n的图形G(n)可以由以下递归式子表示:
G(n - 1)
G(n - 1) G(n - 1)
设递归函数void draw(int n,int x,int y)表示在(x,y)位置开始设置度数为n的图形,它由3个度数为n-1的图形组成,其起始位置分别为:(x,y+2n-2)、(x+2n-2,y)和(x+2n-2,y+2n-1)。
该递归函数的结束条件是:当n=1时(即度数为1的图形),只需在(x,y)位置设置一个字符‘*‘即可。
(2)源程序。
#include <stdio.h>
#define N 70
void f(char a[][N], int rank, int row, int col)
{
if(rank==1){
a[row][col] = ‘*‘;
return;
}
int w = 1;
int i;
for(i=0; i<rank-1; i++) w *= 2;
f(a, rank-1, row, col+w/2);
f(a, rank-1, row+w/2, col);
f(a, rank-1, row+w/2, col+w);
}
int main()
{
char a[N][N],x,w;
int i,j;
for(i=0;i<N;i++)
for(j=0;j<N;j++) a[i][j] = ‘ ‘;
scanf("%d",&x);
w=1;
for(i=0; i<x-1; i++) w *= 2;
f(a,x,0,0);
for(i=0; i<w; i++){
for(j=0; j<2*w; j++) printf("%c",a[i][j]);
printf("\n");
}
return 0;
}
【例3】Fractal(POJ 2083)。
Description
A fractal is an object or quantity that displays self-similarity, in a somewhat technical sense, on all scales. The object need not exhibit exactly the same structure at all scales, but the same "type" of structures must appear on all scales.
A box fractal is defined as below :
A box fractal of degree 1 is simply
X
A box fractal of degree 2 is
X X
X
X X
If using B(n - 1) to represent the box fractal of degree n - 1, then a box fractal of degree n is defined recursively as following
B(n - 1) B(n - 1)
B(n - 1)
B(n - 1) B(n - 1)
Your task is to draw a box fractal of degree n.
Input
The input consists of several test cases. Each line of the input contains a positive integer n which is no greater than 7. The last line of input is a negative integer −1 indicating the end of input.
Output
For each test case, output the box fractal using the ‘X‘ notation. Please notice that ‘X‘ is an uppercase letter. Print a line with only a single dash after each test case.
Sample Input
3
4
-1
Sample Output
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
-
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
-
(1)编程思路。
度数为n的图形,其大小是3^(n-1)*3^(n-1),可以用字符数组来存储图形中各个字符,因为n<=7,而3^6=729,因此可以定义一大小为731*731的字符数组来存储度数不超过7的图形。
度数为n的图形可以有以下递归式子表示:
B(n - 1) B(n - 1)
B(n - 1)
B(n - 1) B(n - 1)
设递归函数void draw(int n,int x,int y)表示在(x,y)位置开始设置度数为n的图形,它由5个度数为n-1的图形组成,其起始位置分别为:(x,y)、(x,y+2*s)、(x+s,y+s)、(x+2*s,y)和(x+2*s,y+2*s),其中s=3^(n-2)。
该递归函数的结束条件是:当n=1时(即度数为1的图形),只需在(x,y)位置设置一个字符‘X‘即可。
(2)源程序。
#include<iostream>
#include<cmath>
using namespace std;
char map[731][731];
void draw(int n,int x,int y)
{
int size;
if(n==1)
{
map[x][y]=‘X‘;
return ;
}
size=pow(3.0,n-2);
draw(n-1,x,y); //左上角
draw(n-1,x,y+2*size); //右上角
draw(n-1,x+size,y+size); //中间
draw(n-1,x+2*size,y); //左下角
draw(n-1,x+2*size,y+2*size); //右下角
}
int main()
{
int i,j,n,size;
while(cin>>n && n!=-1)
{
size=pow(3.0,n-1);
for(i=1;i<=size;i++)
{
for(j=1;j<=size;j++)
map[i][j]=‘ ‘;
}
draw(n,1,1);
for(i=1;i<=size;i++)
{
for(j=1;j<=size;j++)
cout<<map[i][j];
cout<<endl;
}
cout<<"-\n";
}
return 0;
}
原文:https://www.cnblogs.com/cs-whut/p/11096348.html