1 特征选择
特征选择的理解:在决策树算法中,每次选择一个最优的特征来分支是最最重要的一步,那究竟如何选择这个最优的特征就变成了关键问题。对于拿到的数据中,什么类别标签的样本都有,是十分不确定的,换句话说就是十分混乱的。你用数据中其中一个特征来划分数据之后,数据的混乱程度都会变小,最优的划分特征就是通过此特征划分之后数据的混乱程度变的最小的那一个特征。下面分别介绍两种选取最优划分特征的算法,信息增益和信息增益率。
2 信息增益
为了引出信息增益算法,首先定义出信息熵,联合熵和条件熵的概念。
信息熵为信息论中的概念,熵表示随机变量不确定性的度量,即信息熵越大的事物,它的不确定性就越大,对于随机变量X公式如下:
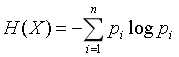
其中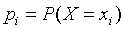 ,意思是:随机变量X的取值为Xi 时的概率。n为X有n种取值。
,意思是:随机变量X的取值为Xi 时的概率。n为X有n种取值。
举个栗子,假如X的取值只有0和1,则X的分布为:
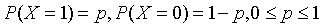
则X的熵为:
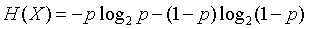
第二个概念是联合熵,设有两个随机变量X和Y,其联合熵为:
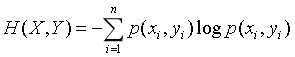
第三个概念是条件熵,对于条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。同时可定义为Y在给定条件X下Y的条件概率分布的熵对X的数学期望,公式如下:
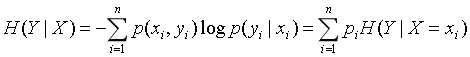
其中pi = P(X = xi),i = 1, 2, 3, ..., n。
下面主角就可以登场了,信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度,通俗来说就是某事件的信息熵与以某个特征为条件的条件熵之差。
特征A对训练数据集D的信息增益g(D, A),定义为集合D的经验熵与特征A给定条件下D的条件熵H(D|A)之差,公式为:
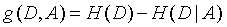
信息增益也叫互信息,决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
决策树学习应用信息增益的准则选择特征,给定训练数据集D和特征A,经验熵H(D)表示对数据集D进行分类的不确定性。而经条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性,那么他们的差就是信息增益,就表示由于特征A而使得对数据集D的分类的不确定性减少的程度。显然,对于数据集D而言,信息增益依赖于特征,不同的特征往往具有不同的信息增益,信息增益大的特征具有更强的分类能力。
下面再次举一个栗子,每个样本有三个特征,第一个是是否有房,第二个特征是婚姻状况,有三个可能:单身,已婚,离异,第三个特征是年收入,是一个连续值,标签是是否拖欠贷款,是一个二分类问题,样本如下:
| 是否有房 | 婚姻状况 | 年收入 | 是否拖欠贷款 |
| 是 | 单身 | 125k | 否 |
| 否 | 已婚 | 100k | 否 |
| 否 | 单身 | 70k | 否 |
| 是 | 已婚 | 120k | 否 |
| 否 | 离异 | 95k | 是 |
| 否 | 已婚 | 60k | 否 |
| 是 | 离异 | 220k | 否 |
| 否 | 单身 | 85k | 是 |
| 否 | 已婚 | 75k | 否 |
| 否 | 单身 | 90k | 是 |
根据是否有房计算信息增益:
首先计算样本的经验熵: 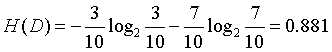
然后计算在是否有房的特征(A)下计算条件经验熵:
有房的经验熵: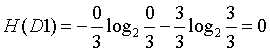
无房的经验熵: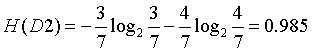
特征A下的条件经验熵: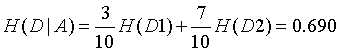
最后计算信息增益: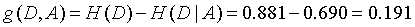
3 信息增益率
以信息增益作为划分训练集特征有些缺点:它偏向于选择取值较多的特征。而使用信息增益率可以对这一问题进行校正,可以作为另一个特征选择的准则。
对于数据集D和某一特征A,则特征A对训练集D的信息增益比gR(D, A)定义为:其信息增益与训练数据集D关于特征A的熵HA(D)之比,即:
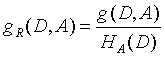
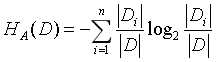
其中n为特征A的取值个数,|D|为数据集D的样本个数,|Di|为样本的特征A第i个取值的样本个数。
4 ID3决策树生成
决策树生成方法:从根节点开始,在根节点上有所有的样本,然后对样本计算所有特征的信息增益,选取信息增益最大的特征作为节点的特征,并用特征的不同的取值建立子节点;再对子节点递归的调用以上方法,构建决策树;直到所有特征的信息增益都很小或没有特征可以选择。
ID3决策树生成算法:
输入:训练数据集D,特征集A,阈值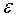
输出:决策树T
(1)若训练集D中所有的样本属于同一类Ck,则T为单节点树,并将类Ck作为该结点的类标记,返回树T;
(2)若特征集A为空集合,则T为单结点树,并将D中样本数最多的类Ck作为该结点的类标记,返回数T;
(3)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征Ag;
(4)如果Ag的信息增益小于阈值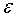 ,则置T为单结点树,并将D中样本数最大的类Ck作为该结点的类标签,返回树T;
,则置T为单结点树,并将D中样本数最大的类Ck作为该结点的类标签,返回树T;
(5)否则,对Ag的每一个可能的值ai,按照Ag=ai将D分割成若干非空子集Di,将Di中样本数最多的类作为标签,构建子结点,由结点及其子结点构成树T,返回T;
(6)对第i个子结点,以Di作为训练集,以A-{Ag}作为特征集,递归的调用步(1)~(5),得到子树Ti,返回Ti。
ID3算法并没有对过解决过拟合问题。
5 C4.5决策树的生成
C4.5对算法进行改进,将信息增益改为信息增益率作为选择最优特征的准则
C4.5决策树生成算法:
输入:训练数据集D,特征集A,阈值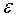
输出:决策树T
(1)若训练集D中所有的样本属于同一类Ck,则T为单节点树,并将类Ck作为该结点的类标记,返回树T;
(2)若特征集A为空集合,则T为单结点树,并将D中样本数最多的类Ck作为该结点的类标记,返回数T;
(3)否则,计算A中各特征对D的信息增益率,选择信息增益率最大的特征Ag;
(4)如果Ag的信息增益率小于阈值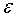 ,则置T为单结点树,并将D中样本数最大的类Ck作为该结点的类标签,返回树T;
,则置T为单结点树,并将D中样本数最大的类Ck作为该结点的类标签,返回树T;
(5)否则,对Ag的每一个可能的值ai,按照Ag=ai将D分割成若干非空子集Di,将Di中样本数最多的类作为标签,构建子结点,由结点及其子结点构成树T,返回T;
(6)对第i个子结点,以Di作为训练集,以A-{Ag}作为特征集,递归的调用步(1)~(5),得到子树Ti,返回Ti。
原文:https://www.cnblogs.com/swenwen/p/11090802.html