? 使用线性回归来为散点作分类
● 代码
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from mpl_toolkits.mplot3d import Axes3D 4 from mpl_toolkits.mplot3d.art3d import Poly3DCollection 5 from matplotlib.patches import Rectangle 6 7 dataSize = 10000 8 trainRatio = 0.3 9 colors = [[0.5,0.25,0],[1,0,0],[0,0.5,0],[0,0,1],[1,0.5,0]] # 棕红绿蓝橙 10 trans = 0.5 11 12 def dataSplit(data, part): # 将数据集分割为训练集和测试集 13 return data[0:part,:],data[part:,:] 14 15 def function(x,para): # 连续回归函数 16 return np.sum(x * para[0]) + para[1] 17 18 def judge(x, para): # 分类函数,用 0.5 作突跃点 19 return int(function(x, para) > 0.5) 20 21 def createData(dim, len): # 生成测试数据 22 np.random.seed(103) 23 output=np.zeros([len,dim+1]) 24 25 if dim == 1: 26 temp = 2 * np.random.rand(len) 27 output[:,0] = temp 28 output[:,1] = list(map(lambda x : int(x > 1), temp)) 29 #print(output, "\n", np.sum(output[:,-1])/len) 30 return output 31 if dim == 2: 32 output[:,0] = 2 * np.random.rand(len) 33 output[:,1] = 2 * np.random.rand(len) 34 output[:,2] = list(map(lambda x,y : int(y > 0.5 * (x + 1)), output[:,0], output[:,1])) 35 #print(output, "\n", np.sum(output[:,-1])/len) 36 return output 37 if dim == 3: 38 output[:,0] = 2 * np.random.rand(len) 39 output[:,1] = 2 * np.random.rand(len) 40 output[:,2] = 2 * np.random.rand(len) 41 output[:,3] = list(map(lambda x,y,z : int(-3 * x + 2 * y + 2 * z > 0), output[:,0], output[:,1], output[:,2])) 42 #print(output, "\n", np.sum(output[:,-1])/len) 43 return output 44 else: 45 for i in range(dim): 46 output[:,i] = 2 * np.random.rand(len) 47 output[:,dim] = list(map(lambda x : int(x > 1), (3 - 2 * dim)*output[:,0] + 2 * np.sum(output[:,1:dim], 1))) 48 #print(output, "\n", np.sum(output[:,-1])/len) 49 return output 50 51 def linearRegression(data): # 线性回归 52 len = np.shape(data)[0] 53 dim = np.shape(data)[1] - 1 54 if(dim) == 1: # 一元 55 sumX = np.sum(data[:,0]) 56 sumY = np.sum(data[:,1]) 57 sumXY = np.sum([x*y for x,y in data]) 58 sumXX = np.sum([x*x for x in data[:,0]]) 59 w = (sumXY * len - sumX * sumY) / (sumXX * len - sumX * sumX) 60 b = (sumY - w * sumX) / len 61 return (w , b) 62 else: # 二元及以上,暂不考虑降秩的问题 63 dataE = np.concatenate((data[:, 0:-1], np.ones(len)[:,np.newaxis]), axis = 1) 64 w = np.matmul(np.matmul(np.linalg.inv(np.matmul(dataE.T, dataE)),dataE.T),data[:,-1]) # w = (X^T * X)^(-1) * X^T * y 65 return (w[0:-1],w[-1]) 66 67 def test(dim): # 测试函数 68 allData = createData(dim, dataSize) 69 trainData, testData = dataSplit(allData, int(dataSize * trainRatio)) 70 71 para = linearRegression(trainData) 72 73 myResult = [ judge(i[0:dim], para) for i in testData ] 74 errorRatio = np.sum((np.array(myResult) - testData[:,-1].astype(int))**2) / (dataSize*(1-trainRatio)) 75 print("dim = "+ str(dim) + ", errorRatio = " + str(round(errorRatio,4))) 76 if dim >= 4: # 4维以上不画图,只输出测试错误率 77 return 78 79 errorP = [] # 画图部分,测试数据集分为错误类,1 类和 0 类 80 class1 = [] 81 class0 = [] 82 for i in range(np.shape(testData)[0]): 83 if myResult[i] != testData[i,-1]: 84 errorP.append(testData[i]) 85 elif myResult[i] == 1: 86 class1.append(testData[i]) 87 else: 88 class0.append(testData[i]) 89 errorP = np.array(errorP) 90 class1 = np.array(class1) 91 class0 = np.array(class0) 92 93 fig = plt.figure(figsize=(10, 8)) 94 95 if dim == 1: 96 plt.xlim(0.0,2.0) 97 plt.ylim(-0.5,1.25) 98 plt.plot([1, 1], [-0.5, 1.25], color = colors[0],label = "realBoundary") 99 xx = np.arange(0,2,0.2) 100 plt.plot(xx, [function(i, para) for i in xx],color = colors[4], label = "myF") 101 plt.scatter(class1[:,0], class1[:,1],color = colors[1], s = 2,label = "class1Data") 102 plt.scatter(class0[:,0], class0[:,1],color = colors[2], s = 2,label = "class0Data") 103 plt.scatter(errorP[:,0], errorP[:,1],color = colors[3], s = 16,label = "errorData") 104 plt.text(0.4, 1.12, "realBoundary: 2x = 1\nmyF(x) = " + str(round(para[0],2)) + " x + " + str(round(para[1],2)) + "\n errorRatio = " + str(round(errorRatio,4)),105 size=15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 106 R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(5)] 107 plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData", "myF"], loc=[0.81, 0.2], ncol=1, numpoints=1, framealpha = 1) 108 109 if dim == 2: 110 plt.xlim(0.0,2.0) 111 plt.ylim(0.0,2.0) 112 xx = np.arange(0, 2 + 0.2, 0.2) 113 plt.plot(xx, [function(i,(0.5,0.5)) for i in xx], color = colors[0],label = "realBoundary") 114 X,Y = np.meshgrid(xx, xx) 115 contour = plt.contour(X, Y, [ [ function((X[i,j],Y[i,j]), para) for j in range(11)] for i in range(11) ]) 116 plt.clabel(contour, fontsize = 10,colors=‘k‘) 117 plt.scatter(class1[:,0], class1[:,1],color = colors[1], s = 2,label = "class1Data") 118 plt.scatter(class0[:,0], class0[:,1],color = colors[2], s = 2,label = "class0Data") 119 plt.scatter(errorP[:,0], errorP[:,1],color = colors[3], s = 8,label = "errorData") 120 plt.text(1.48, 1.85, "realBoundary: -x + 2y = 1\nmyF(x,y) = " + str(round(para[0][0],2)) + " x + " + str(round(para[0][1],2)) + " y + " + str(round(para[1],2)) + "\n errorRatio = " + str(round(errorRatio,4)), 121 size = 15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 122 R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(4)] 123 plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData"], loc=[0.81, 0.2], ncol=1, numpoints=1, framealpha = 1) 124 125 if dim == 3: 126 ax = Axes3D(fig) 127 ax.set_xlim3d(0.0, 2.0) 128 ax.set_ylim3d(0.0, 2.0) 129 ax.set_zlim3d(0.0, 2.0) 130 ax.set_xlabel(‘X‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 131 ax.set_ylabel(‘Y‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 132 ax.set_zlabel(‘W‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 133 v = [(0, 0, 0.5), (0, 0.5, 0), (1, 2, 0), (2, 2, 1.5), (2, 1.5, 2), (1, 0, 2)] 134 f = [[0,1,2,3,4,5]] 135 poly3d = [[v[i] for i in j] for j in f] 136 ax.add_collection3d(Poly3DCollection(poly3d, edgecolor = ‘k‘, facecolors = colors[0]+[trans], linewidths=1)) 137 ax.scatter(class1[:,0], class1[:,1],class1[:,2], color = colors[1], s = 2, label = "class1") 138 ax.scatter(class0[:,0], class0[:,1],class0[:,2], color = colors[2], s = 2, label = "class0") 139 ax.scatter(errorP[:,0], errorP[:,1],errorP[:,2], color = colors[3], s = 8, label = "errorData") 140 ax.text3D(1.62, 2, 2.35, "realBoundary: -3x + 2y +2z = 1\nmyF(x,y,z) = " + str(round(para[0][0],2)) + " x + " + 141 str(round(para[0][1],2)) + " y + " + str(round(para[0][2],2)) + " z + " + str(round(para[1],2)) + "\n errorRatio = " + str(round(errorRatio,4)), 142 size = 12, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1, 0.5, 0.5), fc=(1, 1, 1))) 143 R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(4)] 144 plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData"], loc=[0.83, 0.1], ncol=1, numpoints=1, framealpha = 1) 145 146 fig.savefig("R:\\dim" + str(dim) + ".png") 147 plt.close() 148 149 if __name__ == ‘__main__‘: 150 test(1) 151 test(2) 152 test(3) 153 test(4)
● 输出结果
dim = 1, errorRatio = 0.003 dim = 2, errorRatio = 0.0307 dim = 3, errorRatio = 0.0186 dim = 4, errorRatio = 0.0349
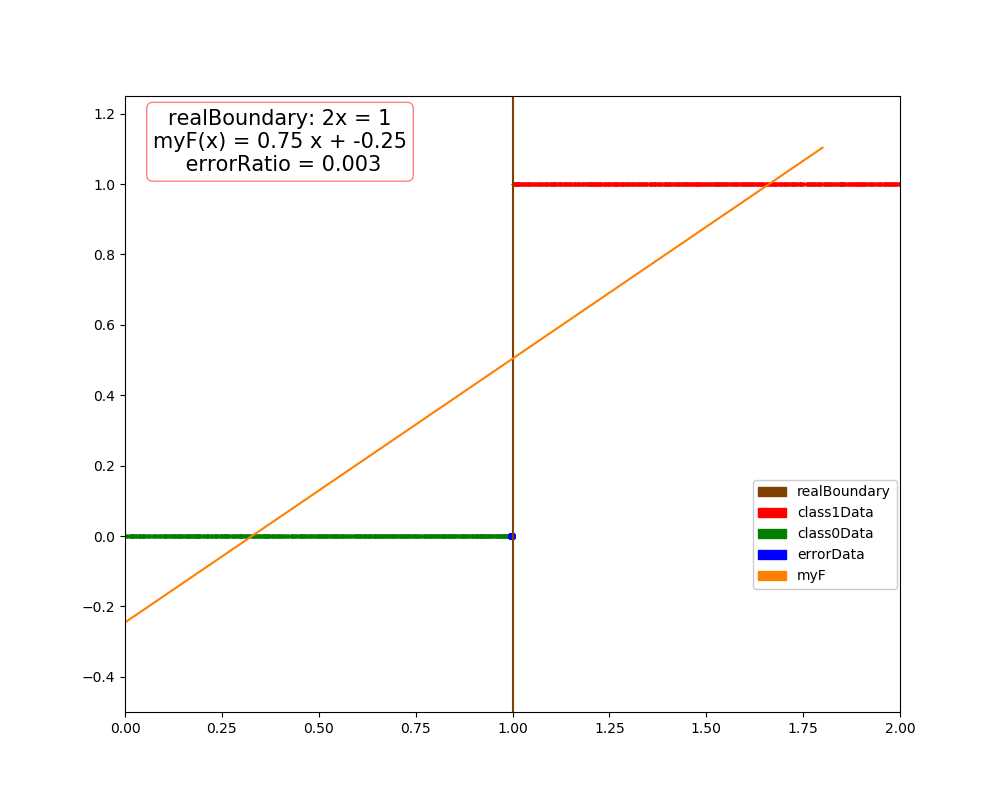
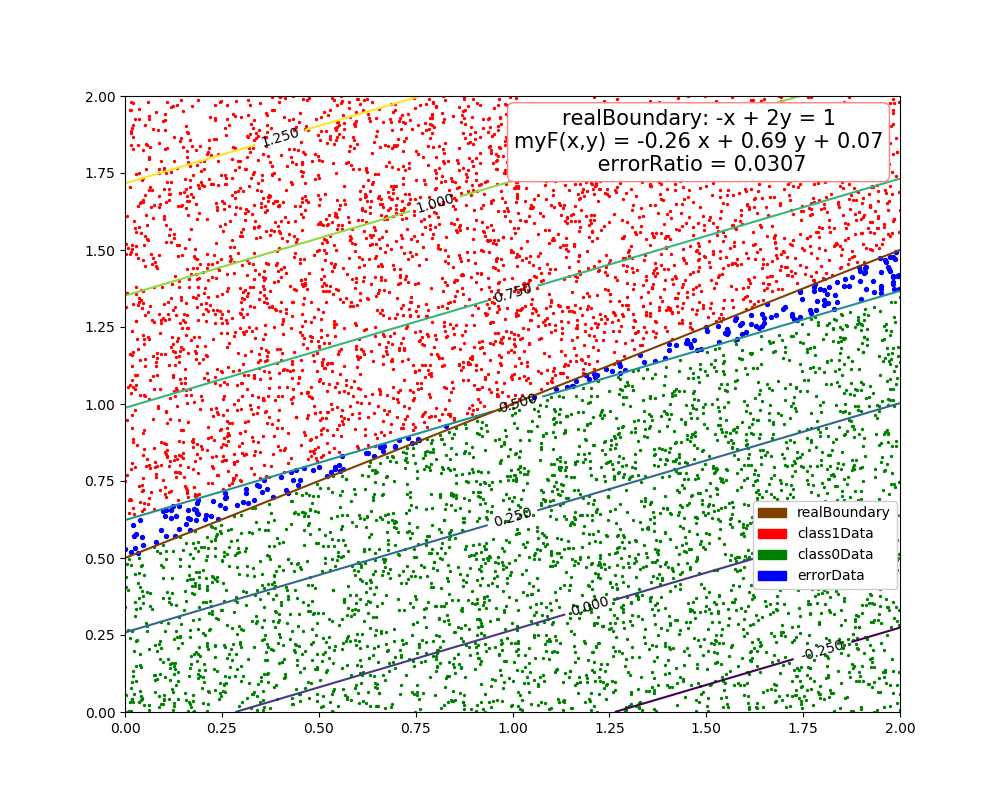
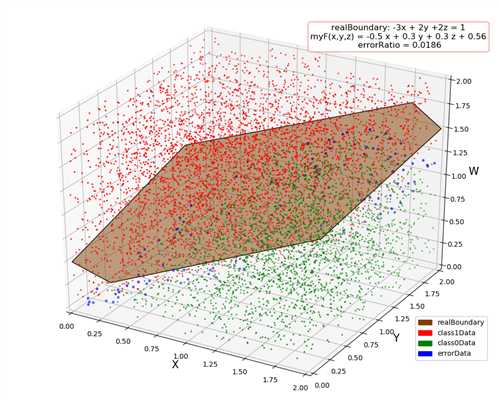
原文:https://www.cnblogs.com/cuancuancuanhao/p/11111014.html