洛谷P5364 [SNOI2017]礼物 题解

传送门

/*
热情好客的小猴子请森林中的朋友们吃饭，他的朋友被编号为 1∼N，每个到来的朋友都会带给他一些礼物：大香蕉。其中，第一个朋友会带给他 11 个大香蕉，之后，每一个朋友到来以后，都会带给他之前所有人带来的礼物个数再加他的编号的K次方那么多个。所以，假设K=2，前几位朋友带来的礼物个数分别是：

1,5,15,37,83,…
假设K=3，前几位朋友带来的礼物个数分别是：

1,9,37,111,…
现在，小猴子好奇自己到底能收到第 \text{N}N 个朋友多少礼物，因此拜托于你了。

已知 N,K，请输出第 N 个朋友送的礼物个数 mod10^9+7。

N<=10^18
K<=10
*/

题面

暴搞通项公式

蒟蒻想了一上午弄出来个$O(k^2)$的算法

这道题比较裸，就是甩给你个递推式让你求第$n$项

$\large A_1 = 1,A_n = \sum_{i=1}^{n-1} A_i + n^k$

那首先我们来手动打个表qwq

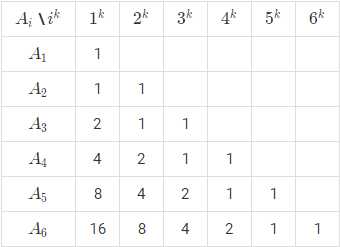
表中第$i$行的系数乘上对应列标后的和就是$A_i$

于是我们发现了这一显然的规律

$\large A_1 = 1,A_n = 2 A_{n-1} + n^k - (n-1)^k$

我们就非常优秀的把这个递推式化简了:p

然而这并没有什么卵用

不过看到这个式子，就总感觉它有个通项公式什么的吧，我们来胡乱瞎推一波

观察递推式，右式那坨$n^k - (n-1)^k$看着就恶心，我们想找个办法把它消掉，使它的形式变成一个等比数列，这样通项公式就容易得到了

显然$n^k - (n-1)^k$是一个$k-1$次多项式，所以我们构造数列$U$和$k-1$次多项式$B$

$\large U_n = A_n + B(n)$

$\large B(n) = \sum_{i=0}^{k-1} b_i n^i$

对数列$U$的定义式移项得

$\large A_n = U_n - B(n)$

带回$A$的递推式，得

$\large U_n - B(n) = 2(U_{n-1} - B(n-1)) + n^k - (n-1)^k$

$\large U_n = 2U_{n-1} + B(n) - 2B(n-1) + n^k - (n-1)^k$

我们想让$U_n=2U_{n-1}$，只需使

$\large B(n) - 2B(n-1) + n^k - (n-1)^k = 0$

即

$\large - B(n) + 2B(n-1) = n^k - (n-1)^k$

现在我们要求解多项式$B$，试着将多项式的每一项，也就是$b_i$，都表示出来

先看右式，用二项式定理展开$(n-1)^k$，右式变为

$\large \quad n^k - \sum_{i=0}^{k} C_k^i (-1)^{k-i} n^i$

提出和式中的$k$次项与$n^k$消掉

$\large = - \sum_{i=0}^{k-1} C_k^i (-1)^{k-i} n^i$

再来看左式，将多项式展开得

$\large \quad - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} b_i (n-1)^i$

也用二项式定理展开$(n-1)^i$

$\large = - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} b_i \sum_{j=0}^i C_i^j (-1)^{i-j} n^j$

转换枚举

$\large = - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} \sum_{j=0}^i b_iC_i^j (-1)^{i-j} n^j$

$\large = - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{j=0}^{k-1} \sum_{i=j}^{k-1} b_iC_i^j (-1)^{i-j} n^j$

将外层的$i$和内层的$j$交换

$\large = - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} \{ \sum_{j=i}^{k-1} b_j C_j^i (-1)^{j-i} \} n^i$

（这里大括号只是为了标明系数，没有实际意义）

现在把左右式合在一起写

$\large - \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} \{ \sum_{j=i}^{k-1} b_j C_j^i (-1)^{j-i} \} n^i = - \sum_{i=0}^{k-1} C_k^i (-1)^{k-i} n^i$

消掉负号

$\large \quad \sum_{i=0}^{k-1} b_i n^i + 2 \sum_{i=0}^{k-1} \{ \sum_{j=i}^{k-1} b_j C_j^i (-1)^{j-i} \} n^i = \sum_{i=0}^{k-1} C_k^i (-1)^{k-i} n^i$

所以

$\large b_i + 2 \sum_{j=i}^{k-1} b_j C_j^i (-1)^{j-i} = C_k^i (-1)^{k-i} n^i$

于是我们非常~~愉快~~艰难的得到了$b_i$的表示，高斯消元即可$b_i$。

仔细观察发现这是个上三角矩阵，所以我们可以直接$O(k^2)$求解！

于是我们解出了多项式$B$。

回过头来看数列$U$的定义，$U_n = A_n + B(n)$

现在解出了$B$，我们又知道$A_1 = 1$，就能知道

$\large U_1 = A_1 + B(1) = B(1) +1$

于是我们得到了数列$U$的完整递推式

$\large U_1=B(1) + 1,U_n=2U_{n-1}$

现在就容易知道$U$的通项公式了，它是

$\large U_n = ( B(1) + 1 )2^{n-1}$

又因为$A_n = U_n - B(n)$，$A$的通项公式就出来了！

$\large A_n = ( B(1) + 1 )2^{n-1} - B(n)$

完了

//洛谷P5364 [SNOI2017]礼物
//Author:sun123zxy
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<ctime>
#include<cstdlib>
#include<queue>
using namespace std;
typedef long long ll;
const ll MOD=1E9+7;

ll QPow(ll x,ll up){//快速幂 
    x%=MOD;
    ll ans=1;
    while(up){
        if(up%2==0){
            x=x*x%MOD;
            up/=2;
        }else{
            ans=ans*x%MOD;
            up--;
        }
    }
    return ans;
}
ll Inv(ll x){//逆元 
    return QPow(x,MOD-2);
}

const ll MXK=2005;
ll fac[MXK],facInv[MXK];
void FacInit(ll n){
    fac[0]=1;for(ll i=1;i<=n;i++) fac[i]=fac[i-1]*i%MOD;//求阶乘 
    facInv[n]=Inv(fac[n]);
    for(ll i=n-1;i>=1;i--) facInv[i]=facInv[i+1]*(i+1)%MOD;//线性求阶乘逆元 
    facInv[0]=1;
}
ll C(ll n,ll k){//组合数 
    if(n<k) return 0;
    return fac[n]*facInv[n-k]%MOD*facInv[k]%MOD;
}

ll N,K;
ll c,B[MXK];//2^(n-1)的系数c和多项式B 
ll GetY(ll x){//获取B(x)
    x%=MOD;
    ll y=0;
    ll xPow=1;
    for(int i=0;i<=K-1;i++){
        y=(y+B[i]*xPow)%MOD;
        xPow=xPow*x%MOD;
    }
    return y;
}
ll mtx[MXK][MXK];
void GetFormula(){
    for(ll i=0;i<=K-1;i++) for(ll j=0;j<=K;j++) mtx[i][j]=0;
    for(ll i=0;i<=K-1;i++){//初始化方程组 
        mtx[i][i]=1;
        for(ll j=i;j<=K-1;j++){
            ll p=-1;if((j-i)%2==0) p=1;
            mtx[i][j]+=(-2*C(j,i)%MOD*p+MOD)%MOD;
        }
        ll p=-1;if((K-i)%2==0) p=1;
        mtx[i][K]=(C(K,i)*p+MOD)%MOD;
    }
    for(ll i=K-1;i>=0;i--){//上三角高斯消元
        B[i]=mtx[i][K]*Inv(mtx[i][i])%MOD;
        for(ll j=i-1;j>=0;j--){
            mtx[j][K]=(mtx[j][K]-B[i]*mtx[j][i]%MOD+MOD)%MOD;
            mtx[j][i]=0;
        }
    }
    c=(GetY(1)+1)+MOD%MOD;
}
int main(){
    cin>>N>>K;
    FacInit(K);
    GetFormula();
    cout<<(c*QPow(2,N-1)%MOD-GetY(N)+MOD)%MOD;
    return 0;
}

View Code

蒟蒻第一次写这么多数学公式，有错误还请指正，，，

搞完了才发现就是洛谷题解上rqy聚聚描述的答案形式

所以说白了只是定量推导了一下而已

就当理性愉悦把，，，

洛谷P5364 [SNOI2017]礼物 题解

原文：https://www.cnblogs.com/sun123zxy/p/luogu5364.html