设有n个大小不等的中空圆盘,按从小到大的顺序从1到n编号。将这n个圆盘任意的迭套在三根立柱上,立柱的编号分别为A、B、C,这个状态称为初始状态。
现在要求找到一种步数最少的移动方案,使得从初始状态转变为目标状态。
移动时有如下要求:
·一次只能移一个盘;
·不允许把大盘移到小盘上面。
输入格式:
文件第一行是状态中圆盘总数;
第二到第四行分别是初始状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号;
第五到第七行分别是目标状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号。
输出格式:
每行一步移动方案,格式为:move I from P to Q
最后一行输出最少的步数。
圆盘总数≤45
每行的圆盘描述是从下到上的圆盘编号
这道题目是经典的汉诺塔问题,没什么技术,但思维难度较高,如果条件判断太多则编码难度也会较高
首先,我们很容易想到一种假算法:(一定要注意它是错的,但对真算法有启发意义)
因为大盘子无法在小盘子上移动,而大盘子移动好之后又不会影响小盘子(这是本题所有操作的前提),故可以从大盘子开始移动。
我们从第N号盘子开始操作,计当前盘子为i号,如果它在原位置,那么就跳过,否则就将1~i-1号盘子都移动到不会动用的盘子,将目标盘子空出,然后将i号盘子放进去。经过N次操作,一定可以完成,但不能保证最优。
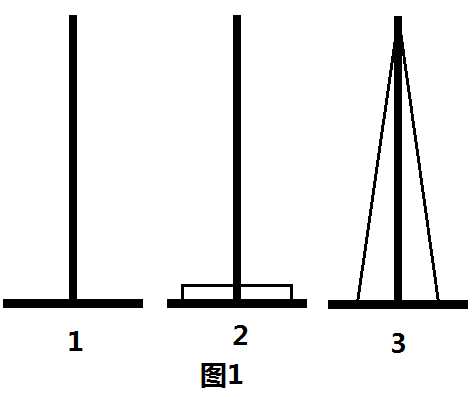
如图所示,如果我们要将第1号桩上的1个大盘子移到2号桩,那么我们就先将1、2号桩上所有比i号盘子小的盘子都移到第3号桩
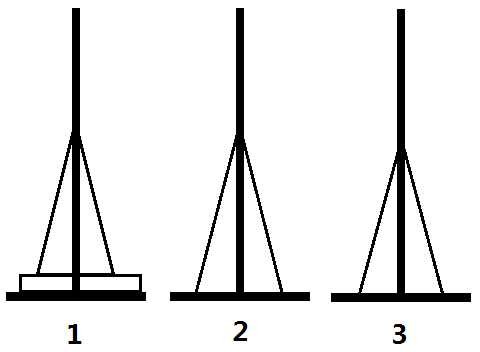
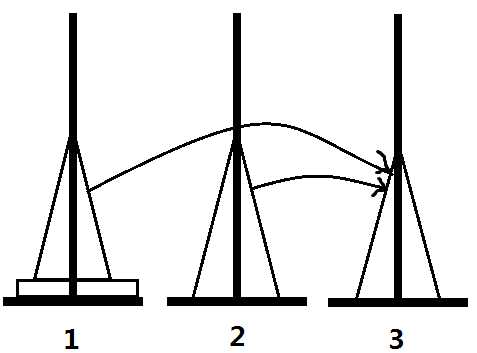

实现这一过程很简单,只要每次将1~i-1号盘子移动到闲置的位置,然后移动即可,代码也十分简单

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const int INF=1e9+7,MAXN=50; 5 int N,cur[MAXN],goal[MAXN],ans; 6 char tran[]={‘ ‘,‘A‘,‘B‘,‘C‘};/*translate*/ 7 inline void input(int *array,int opt){ 8 int ii,jj; 9 scanf("%d",&ii); 10 while(ii--){ 11 scanf("%d",&jj); 12 array[jj]=opt; 13 } 14 } 15 void dfs(int from/*from idx*/,int to/*to pos*/){/*move the "from"-th plate to position "to"*/ 16 if(cur[from]==to) 17 return; 18 int other=6-cur[from]-to; 19 for(int i=from-1;i>=1;i--) 20 dfs(i,other); 21 printf("move %d from %c to %c\n",from,tran[cur[from]],tran[to]); 22 cur[from]=to; 23 ans++; 24 } 25 int main(){ 26 scanf("%d",&N); 27 input(cur,1); 28 input(cur,2); 29 input(cur,3); 30 input(goal,1); 31 input(goal,2); 32 input(goal,3); 33 34 for(int i=N;i>=1;i--) 35 dfs(i,goal[i]); 36 printf("%d",ans); 37 return 0; 38 }
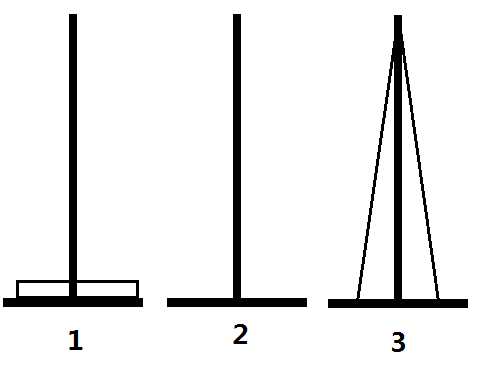
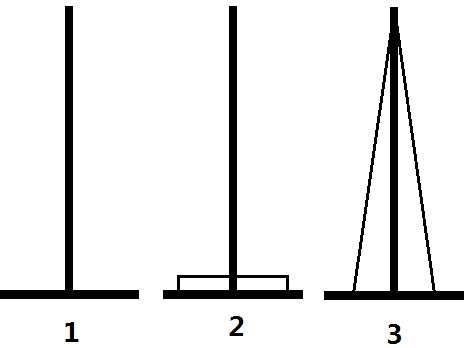
但正如上面所说的,这是一个假算法。我们认定如图的变换方法是正确的,是建立在汉诺塔的性质的基础上的。在汉诺塔中,未归位的盘子都是连续叠加的(如下图1),不可能出现如图2的情况
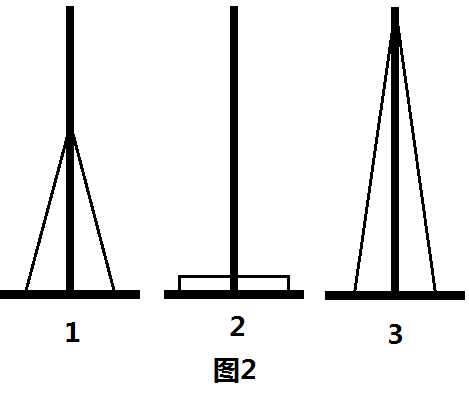
这样的话,无论将这个连续的塔从哪里移动到哪里都是等价的,故开始给出的假算法是成立的。
然而可惜的是,我们的塔最初是随机摆放的,所以会有另一种方法
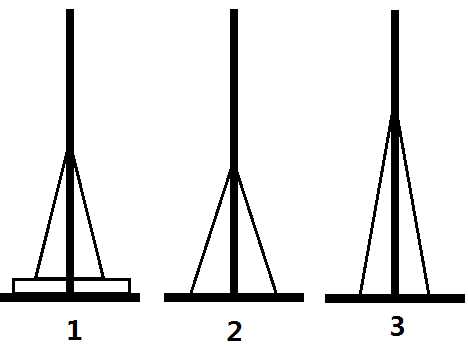
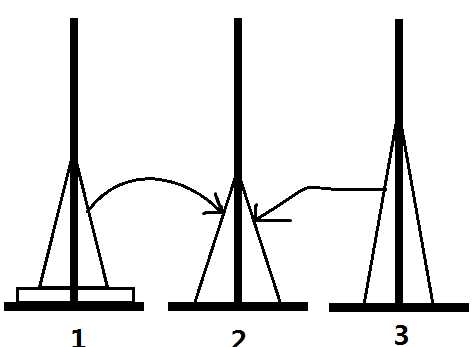
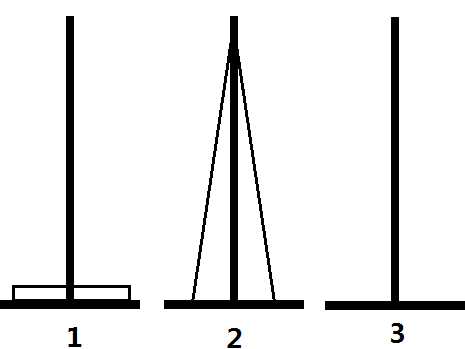
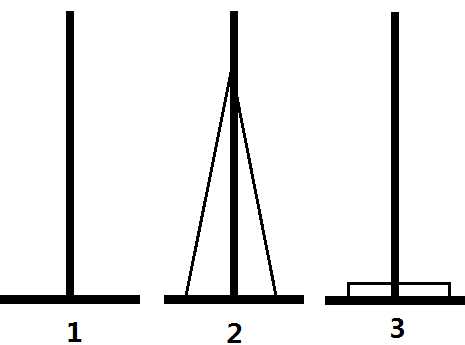

可以证明,没有其他移动方法了。但是否每次都要用两种方法呢?显然不是。观察两个图组可以发现,在进行了一次操作后,就还原到了汉诺塔的基本结构:一串连续的盘子,就可以用常规的方法操作了。
那图组2和图组1的过程又怎么实现呢?我们需要三种操作
move函数的实现很简单,递归将1~idx-1号盘子移到闲置的位置,将idx号盘子移到to,再将1~idx-1号盘子移到to即可
void mov(int idx,int from,int to,int other){ /*move 1~"idx"-th to "to" in a heap*/ if(!idx) return; mov(idx-1,from,other,to); ans[st][++sz[st]]=(state){idx,from,to}; mov(idx-1,other,to,from); }
merge函数也不难,将递归将1~idx-1号盘子移到闲置的位置(用merge),将idx号盘子移到to,再将1~idx-1号盘子移到to即可(用move)
void merg(int idx,int to){ /*move 1~"idx"-th to "to" not in a heap*/ if(!idx) return; if(cur[idx]==to) return merg(idx-1,to); int other=6-cur[idx]-to; merg(idx-1,other); ans[st][++sz[st]]=(state){idx,cur[idx],to}; mov(idx-1,other,to,cur[idx]); }
solve函数的思想同上
void solve(int idx,int to){ /*put 1-"idx"-th into its place*/ if(!idx) return; if(goal[idx]==to) return solve(idx-1,to); int other=6-goal[idx]-to; mov(idx-1,to,other,goal[idx]); ans[st][++sz[st]]=(state){idx,to,goal[idx]}; solve(idx-1,other); }
有了这些操作,解题就很简单了,我们按照上面讲的两种情况分类,输出步数较少的方案即可
void work(int idx){ if(!idx) return; if(cur[idx]==goal[idx]) return work(idx-1); int other=6-cur[idx]-goal[idx]; /*0:all to other, N to to*/ st=0; merg(idx-1,other); ans[st][++sz[st]]=(state){idx,cur[idx],goal[idx]}; solve(idx-1,other); /*1:all to to, N to other, all to from, N to to*/ st=1; merg(idx-1,goal[idx]); ans[st][++sz[st]]=(state){idx,cur[idx],other}; mov(idx-1,goal[idx],cur[idx],other); ans[st][++sz[st]]=(state) {idx,other,goal[idx]}; solve(idx-1,cur[idx]); }
最终给出AC代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const int INF=1e9+7,MAXN=50,MAXP=1e5; 5 int N,cur[MAXN],goal[MAXN],cnt; 6 char tran[]={‘E‘,‘A‘,‘B‘,‘C‘};/*translate*/ 7 inline void input(int *array,int opt){ 8 int ii,jj; 9 scanf("%d",&ii); 10 while(ii--){ 11 scanf("%d",&jj); 12 array[jj]=opt; 13 } 14 } 15 struct state{ int idx,from,to; }ans[2][MAXP]; 16 int st,sz[2]; 17 void mov(int idx,int from,int to,int other){ 18 /*move 1~"idx"-th to "to" 19 in a heap*/ 20 if(!idx) 21 return; 22 mov(idx-1,from,other,to); 23 ans[st][++sz[st]]=(state){idx,from,to}; 24 mov(idx-1,other,to,from); 25 } 26 void merg(int idx,int to){ 27 /*move 1~"idx"-th to "to" 28 not in a heap*/ 29 if(!idx) 30 return; 31 if(cur[idx]==to) 32 return merg(idx-1,to); 33 int other=6-cur[idx]-to; 34 merg(idx-1,other); 35 ans[st][++sz[st]]=(state){idx,cur[idx],to}; 36 mov(idx-1,other,to,cur[idx]); 37 } 38 void solve(int idx,int to){ 39 /*put 1-"idx"-th into its place*/ 40 if(!idx) 41 return; 42 if(goal[idx]==to) 43 return solve(idx-1,to); 44 int other=6-goal[idx]-to; 45 mov(idx-1,to,other,goal[idx]); 46 ans[st][++sz[st]]=(state){idx,to,goal[idx]}; 47 solve(idx-1,other); 48 } 49 void work(int idx){ 50 if(!idx) 51 return; 52 if(cur[idx]==goal[idx]) 53 return work(idx-1); 54 int other=6-cur[idx]-goal[idx]; 55 /*0:all to other, N to to*/ 56 st=0; 57 merg(idx-1,other); 58 ans[st][++sz[st]]=(state){idx,cur[idx],goal[idx]}; 59 solve(idx-1,other); 60 /*1:all to to, N to other, all to from, N to to*/ 61 st=1; 62 merg(idx-1,goal[idx]); 63 ans[st][++sz[st]]=(state){idx,cur[idx],other}; 64 mov(idx-1,goal[idx],cur[idx],other); 65 ans[st][++sz[st]]=(state) {idx,other,goal[idx]}; 66 solve(idx-1,cur[idx]); 67 } 68 int main(){ 69 scanf("%d",&N); 70 input(cur,1); 71 input(cur,2); 72 input(cur,3); 73 input(goal,1); 74 input(goal,2); 75 input(goal,3); 76 77 work(N); 78 79 for(int i=1,ed=min(sz[0],sz[1]),j=sz[0]>sz[1];i<=ed;i++) 80 printf("move %d from %c to %c\n",ans[j][i].idx,tran[ans[j][i].from],tran[ans[j][i].to]); 81 printf("%d",min(sz[0],sz[1])); 82 return 0; 83 }
原文:https://www.cnblogs.com/guoshaoyang/p/11114054.html