卡尔曼滤波

什么是卡尔曼滤波

对于这个滤波器，我们几乎可以下这么一个定论：只要是存在不确定信息的动态系统，卡尔曼滤波就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰，卡尔曼滤波通常也能很好的弄清楚究竟发生了什么，找出现象间不易察觉的相关性。

因此卡尔曼滤波非常适合不断变化的系统，它的优点还有内存占用较小（只需保留前一个状态）、速度快，是实时问题和嵌入式系统的理想选择。

形象解释

卡尔曼滤波就是以上个时刻的状态，推断下个时刻的状态。

比如一个有经验的船长，没有很先进的仪器能定位船的位置，他需要走一会判断一下位置，然后根据这个位置判断下一个位置，否则走的太远就迷路了；

首先他能知道起点的位置，然后每隔一定时间，就根据船速、航线、风向等预估自己的位置，这是经验，不一定准确，且肯定存在一定误差；

他还有个不太精确的仪器，能测量出自己的位置，也不一定准确，且也存在一定误差；

那现在有了经验值和测量值，到底哪个准确，如何参考这两个值；

如果船长很自信，更相信自己的经验，这样 经验值的权重就大一些，观测值权重小一些；

如果船长经验不足，肯定不能过分相信经验，只能更多参考测量值，此时测量值权重大一些；

最后就确定了 新的位置X_new

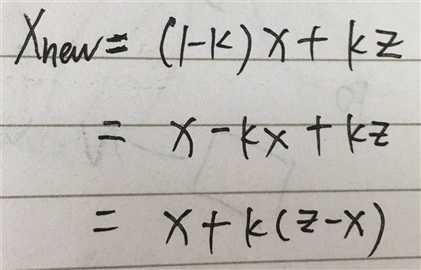
x 为预测， z 为观测

显然 k 决定了各自的权重，那么 k 又是如何确定呢？

我们就看谁更准，怎么做呢？

比如现在真实的位置我们知道，然后拿仪器测，如果结果一样，那说明仪器准，此外由于存在系统误差，如仪器不灵光，外部温度不同，电量不足等等，总之会有一定的误差，每次测量结果可能不太一样，那就需要多测几次，看看结果准不准，也就是计算方差大小，方差大小决定了可信度；

同样的方法人也一样，可以获得人的可信度；

显然 k 就是可信度占比

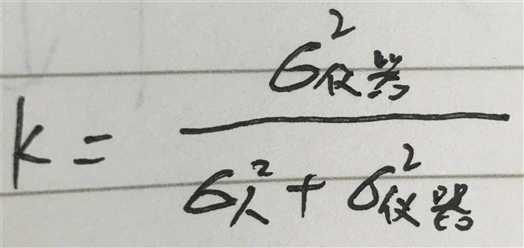
但是要注意一点，可信度随着状态的转移会发生变化，如人在一个熟悉的环境中，他判断位置就会比较准确，在一个陌生的环境中，判断位置就不太可信；

此时 新的位置X_new 似乎确定了，但是别忘了，仍然是 “推测” 的，也不完全准确，也存在一定的偏差，此时的偏差也跟 k 有关，因为 k 实际上决定了 X_new 的精度。

数学建模

卡尔曼滤波有两个假设

1. 世界上噪声无处不在，状态本身有噪声，状态转移也有噪声 ====> 比如现在的测量温度是 30 度，实际上可能是29度，这就是状态噪声；你开空调1分钟，可能变成25度，也可能变成26度，这就是状态转移噪声

2. 一个系统会处于各种不同的状态，并且可以相互转换，我们无法获取当前状态，但是可以通过测量猜测出当前状态

场景描述

有一辆小车在行进，车上装有传感器获取 速度v，也装有定位装置获取 位置p，那么小车的状态就可以用 x=[p, v]’ 来表示；

在车行驶的过程中，存在内部控制，如踩油门加速；也存在外部影响，如风阻

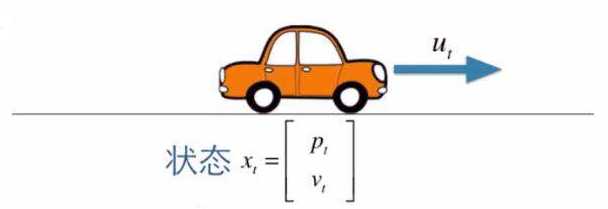
u 可以理解为加速度；

######## 得到 某时刻的状态

误差表示

卡尔曼滤波假设噪声无处不在，仪器获取的数据当然也有噪声，所以我们只能认为 测量值是真实值的最优估计，并且误差服从正态分布，

我们用 最优估计 代表当前状态，但是实际上真实的状态是某个范围中的一点

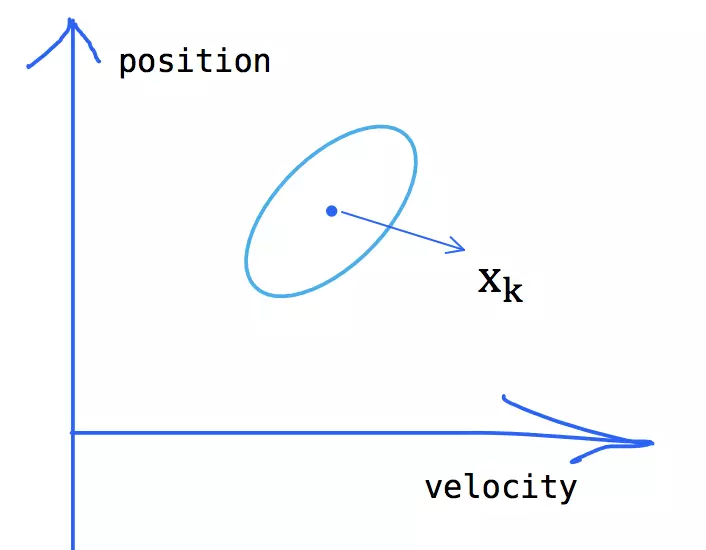
x_k就是最优估计，其实就是均值，这里记住状态是均值；

其周围的部分就是方差，由于是两个量，车速和位置，所以用协方差表示

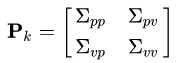
这就是当前状态的方差，即当前状态的可信度

######## 得到 该时刻的状态 的方差，形成 该时刻状态 的 高斯分布

状态转移

根据物理公式可以得到 下一时刻的 位置p_t 和 速度v_t，并转换成矩阵的表示方式，在形式上做简化，就得到如下公式。

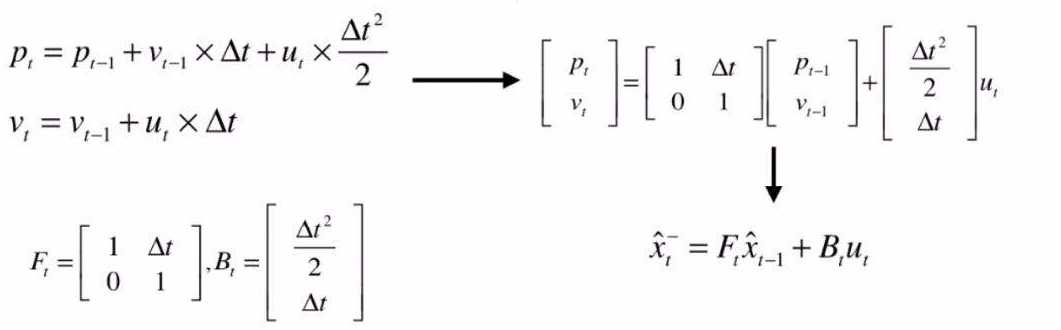
其中 F_t 代表状态转移矩阵；B_t 代表状态控制矩阵；u_t 代表 状态控制向量

状态-均值发生变化，其方差也会相应转变

P_t = F_tP_t-1F_t^T，T表示转置　　　　　　　　【协方差矩阵的性质  cov(Ax, Bx)=Acov(x, y)B^T】

形成了新的高斯分布

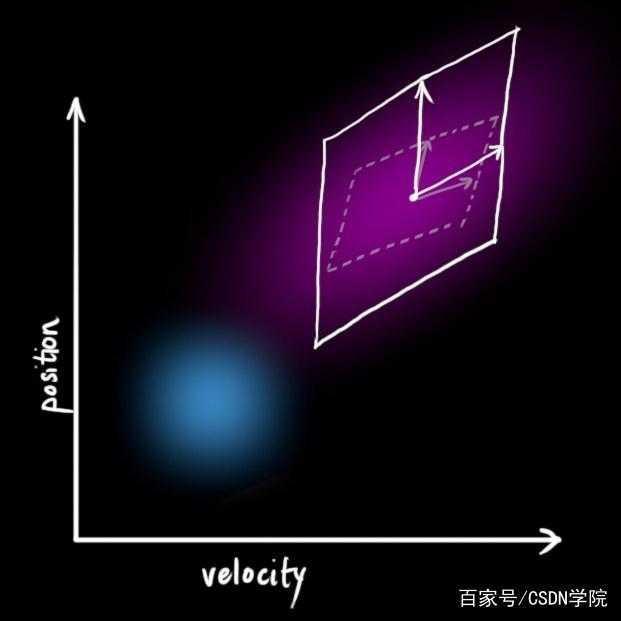
考虑到外部影响因素，这里假设外部影响因素服从 高斯分布 w_k~N(0, Q_k)　　　　　　【一会顺风，一会逆风，一会上坡，一会下坡，可以看做均值为0的正态分布】

至此得到完整的状态预测方程

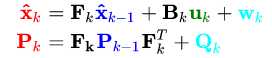
状态是均值，由于 w_k 均值为0，有些教程直接忽略了，具体使用时根据实际情况而定； 

######## 得到 下一时刻的状态 的预测 和 对应的方差，形成 下一时刻状态 的 高斯分布，并带噪声

状态转换成指标

小车的状态是 车速 和 位置，但是状态可能不是我们需要的数学指标，所以需要进行转换，如观测到你出汗了，但我们需要你热不热，此时就把出汗转换成热；

假设这个转换矩阵为 H_k；

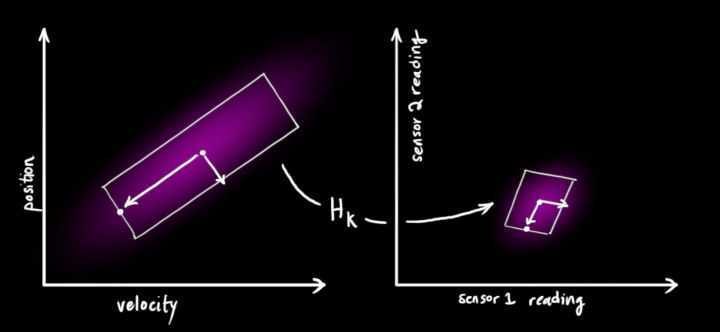
上步得到的 下一时刻状态的 预测和方差就要转换成

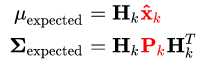
此时我们完成了下一状态的预测，结果服从正态分布

######## 得到 下一时刻指标 的预测 和 对应的方差，形成 下一个时刻指标的 高斯分布，带噪声

状态观测

用传感器观测小车的状态，车速和位置，也是带有误差的，转换成数学指标，

把 协方差 记作 R_k，把状态的数学指标记为 Z_k，即均值

权衡分析

现在有了 下一时刻 的预测值和观测值，和对应方差，如下图

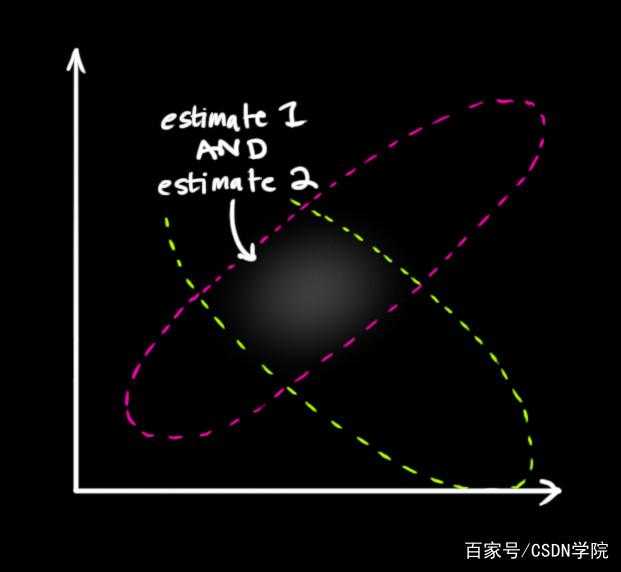
这就可以根据方差来确定 k (形象描述里面的k)，然后计算这个时刻的 最优估计状态，并更新方差

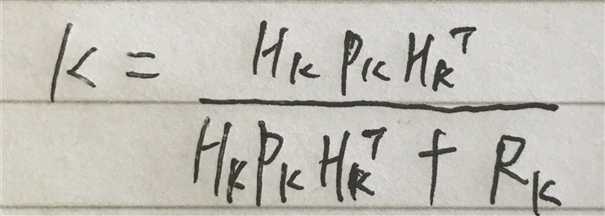
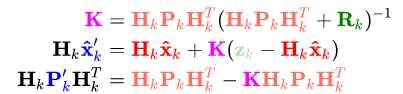
为了简化式子，把上面三个式子都 左乘 H_k^-1

第三个式子再 右乘 H_k 的转置的逆，得到如下式子

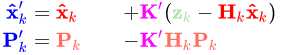
这就得到了 下一个时刻 的状态和噪声

此时就可以继续预测下下时刻的状态 和噪声。

总结

卡尔曼滤波就是5个公式

预测，更新，更新完在预测

图形描述

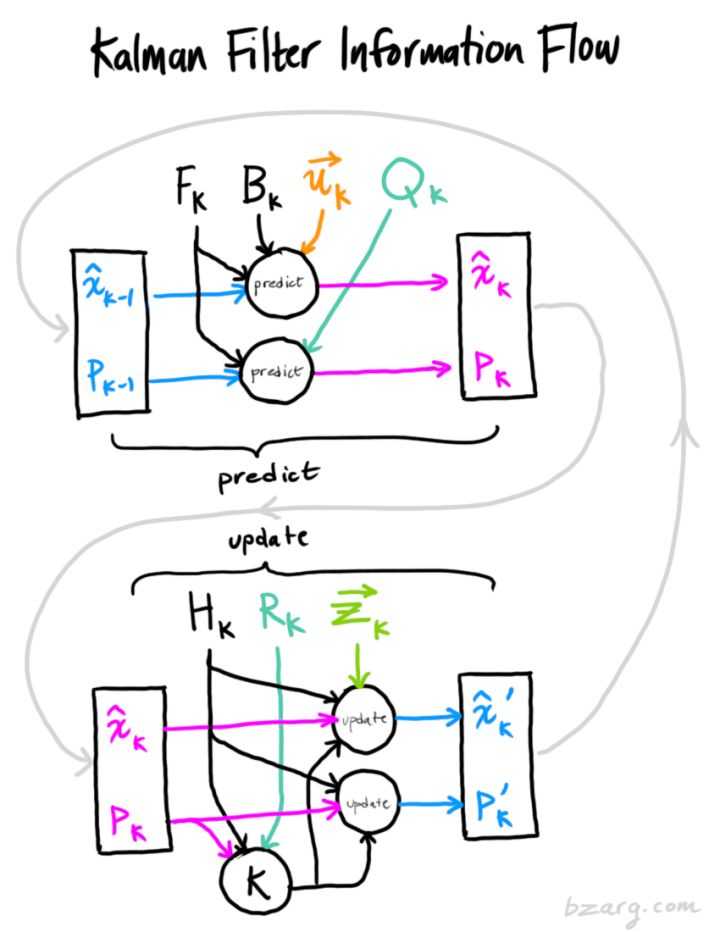
参考资料：

https://zhuanlan.zhihu.com/p/39912633　　　　更详尽请参考该教程

https://www.zhihu.com/question/22422121/answer/22877882

https://blog.csdn.net/guo1988kui/article/details/82778198

卡尔曼滤波

原文：https://www.cnblogs.com/yanshw/p/11127628.html